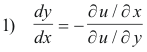
Prove that the curves of the family u(x, y) = c are the orthogonal trajectories of the curves of the family v(x, y) = k.

Proof. Implicit differentiation gives the slope of the general curve of the family u(x, y) = c as

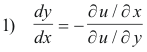
and the slope of the general curve of the family v(x, y) = k as

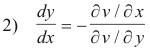
Since w = f(z) = u(x, y) + iv(x, y) is an analytic function, u(x, y) and v(x, y) must satisfy the Cauchy-Riemann equations

Using these, 2) can be written as

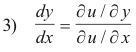
From 1) and 3) we see that, at any common point, the slope of the general curve of the family v(x, y) = k is the negative reciprocal of the slope of the general curve of the family u(x, y) = c. This proves that they are orthogonal trajectories since the condition for two lines with slopes m₁ and m₂ to be perpendicular is that m₁ = -1/m₂.