Prove the following theorem:

Theorem. Both the real part u and the imaginary part v of an analytic function

            f(z) = u(x, y) + iv(x, y)

satisfy Laplace’s equation i.e.

providing the second partial derivatives exist and are continuous.

Proof. If f(z) = u + iy is analytic in a region R then the Cauchy-Riemann equations

are satisfied in R. Assume u and v have continuous second partial derivatives. Differentiating both sides of 1) with respect to x gives

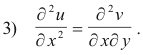
Differentiating both sides of 2) with respect to y gives

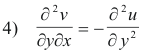
From 3) and 4) we get

In a similar way we can differentiate both sides of 1) with respect to y and 2) with respect to x and obtain