Functions, mappings, limits, continuity, sequences, series

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Functions, mappings, limits, continuity, sequences, series.

Def. Variable. A symbol, such as x, that can stand for any one of a set of numbers. Any member of the set is a value of the variable and the set itself is the range of the variable. A symbol, such as z, that can stand for any one of a set of complex numbers is called a complex variable.

Def. Function (of a variable). If to each value that some variable x can assume there corresponds one or more values of a variable y, we say y is a function of x and write y = f(x) or y = F(x), etc. The variable x is called the independent variable and the variable y is called the dependent variable. The value of a function y = f(x) at x = a is written f(a).

Example 1. The formula A = πr² is a function giving the area A of a circle as a function of its radius r. It assigns to each value of r an area A.

Example 2. The function w = 5z² + 2z + 1, where z is a complex number, supplies to any specified value of z, a value of w i.e. it assigns a complex number w to the complex number z.

Single and multiple-valued functions. If, in a function y = f(x), only one value of y corresponds to each value of x, the function is said to be single-valued. If more than one value of y corresponds to a single value of x, the function is said to be multiple-valued. A multiple-valued function can be viewed as a collection of single-valued functions with each of the single-valued functions regarded as a branch of the multiple-valued function.

Example 1. If we solve the equation y² - x² = 1 we obtain

This function is multiple-valued with the two branches

Example 2. The function

where z is a complex number, is a multiple-valued function with five branches, one branch for each of the five roots of z.

Often one of the branches of a multiple-valued function is selected and regarded as the principal branch.

Generally speaking, multiple-valued functions are regarded as collections of single-valued functions and when we speak of functions we assume them to be single-valued. The two central concepts in the theory of functions of a complex variable are the concepts of the derivative and integral of a complex-valued function. Both of these concepts presume a function that is single-valued. Whenever we speak of a derivative or an integral of a complex-valued function, we tacitly assume it is single-valued.

Inverse functions. If y = f(x), then we can generally, for some interval of interest, also view x as a function of y, x = g(y), or x = f ^-1(y). The function x = g(y), or x = f ^-1(y), is called the inverse of the function y = f(x).

A function has an inverse if and only if it is one-to-one.

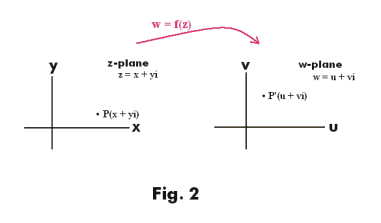
Graphs of functions of a complex variable. The reader is presumably familiar with the graphical representation of a function y = f(x) of a real variable i.e. a graphical representation such as that shown in Fig. 1. Such a graphical representation is very helpful for giving an intuitive feel for how the function behaves. We ask a question. How can one depict graphically a function of a complex variable i.e. a function y = f(x) when x and y are complex numbers? Such a representation would be very helpful for understanding the behavior of functions of complex variables. It is done as follows: We employ two Cartesian coordinate systems. Let us say we want to plot the function w = f(z) where z = x + yi and w = u + vi. We label one coordinate system the z-plane and the other coordinate system the w-plane as shown in Fig. 2. We then plot values of z in the z-plane and values of w in the w-plane. In Fig. 2, point P(x + yi ) in the z plane is imaged into point P'(u + vi) in the w-plane. As the independent variable z meanders through some path in the z-plane, the dependent variable w meanders through some path in the w-plane. See Fig. 3. Thus we see that a function of a complex variable w = f(z) effects a mapping from the z-plane to the w-plane — a 2-space to 2-space mapping.

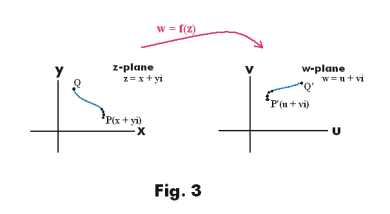
We note that in the case of a function of a real variable (Fig. 1) the independent variable has only one degree of freedom i.e. it is constrained to movement along a straight line (the x-axis) whereas in the case of a function of a complex variable the independent variable has two degrees of freedom i.e. it can move in any direction in the complex plane.

General 2-space to 2-space mapping. The system

u = u(x, y)

v = v(x, y) ,

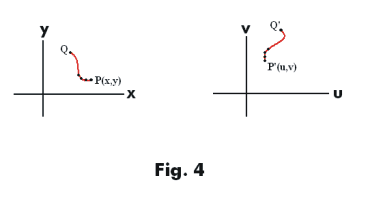
where x, y, u, v are real numbers, effects a mapping from the xy-plane into the uv-plane. It represents the general 2-space to 2-space mapping (or point transformation). It maps a point P(x, y) in the xy-plane into point P'(u, v) in the uv-plane. See Fig. 4. For more information on this transformation see the following:

Point transformations

General mapping of w = f(z). We represent the general function of a complex variable by w = f(z). If z = x + yi, on expansion of f(x + yi) we obtain w = u + iv where

u = u(x, y)

v = v(x, y)

i.e. it is a special case of a 2-space to 2-space mapping. The function f(z) is called the mapping function. A complex function f(z) may have multiple values at only some points in the z-plane and single values at the rest. If it has multiple values at any point in the z-plane it is regarded as being multiple-valued.

*******************************************

Sequences, series, limits, continuity.

*******************************************

Sequences and series of complex terms. A sequence of real numbers is one thing. A sequence of complex numbers is another thing. Real numbers and complex numbers are two different animals. We know what we mean when we speak of the convergence of a sequence of real numbers but what do we mean when speaking of the convergence of a sequence of complex numbers? We are familiar with a sequence of the type

1/2, 1/4, 1/8, ... , 1/2n, ....

(where n is an integer) but how do we deal with a sequence of type

1/2 + 1/2 i, 1/4 + 2/5 i, 1/8 + 3/10 i, ... , 1/2n + [n/(n² + 1)] i, + .... ?

An infinite sequence of real numbers is a sequence of type

a₁, a₂, ... , a_n, ...

while an infinite sequence of complex numbers is a sequence of type

a₁ + ib₁, a₂ + ib₂, ... , a_n + ib_n, ....

How do you measure and determine convergence for an infinite sequence of complex numbers? The answer is that complex numbers can be identified with points in the plane and we view a sequence of complex numbers as a sequence of points. In the sequence of complex numbers

z₁, z₂, ... , z_n, ....

the difference z_i - z_i-1 corresponds to a vector from z_i-1 to z_i-1 and the length of that vector is the distance between the two points. Thus |z_i - z_i-1| gives the distance between successive points in the sequence. Keeping this fact in mind we can apply most of the rules, laws and theorems for sequences and series of real numbers to those of complex numbers with little or no re-wording. The definitions and theorems for the topics of limits, continuity, sequences and series for complex variables read essentially the same as do those for a real variable. One must simply keep in mind that in referring to numbers and variables one is speaking of complex numbers and variables and not real ones.

Theorem 1. A necessary and sufficient condition that the sequence

a₁ + ib₁, a₂ + ib₂, ... , a_n + ib_n, ....

converge is that the sequences

a₁, a₂, ... , a_n, ...

and

b₁, b₂, ... , b_n, ...

converge.

Theorem 2. A necessary and sufficient condition that the series Σ (a_n + ib_n) converge, where a_n and b_n are real, is that the series Σ a_n and Σ b_n converge.

See the following for information on sequences and series:

Sequences

Series

Limits. A function f(z) of a complex variable z is said to approach the complex number b as a limit, when z approaches a, if the value of |f(z) - b| becomes arbitrarily small for values of z sufficiently close to a. This can be written

which is read “the limit of f(z) as z approaches a is b”. Stated more rigorously, a function f(z) approaches the limit b as z approaches a if, for every positive real number ε, however small, there exists a positive real number δ such that |f(z) - b| < ε if 0 < |z-a| < δ.

A function f(z) approaches a limit b as z approaches infinity, i.e.

if for any ε > 0, however small, we can find M > 0 such that |f(z) - b| < ε whenever |z| > M.

We say that a function f(z) approaches infinity as z approaches a i.e.

if for any N > 0, we can find δ > 0 such that |f(z)| > N whenever 0 < |z-a| < δ.

A function may or may not approach a limit as the independent variable approaches a limit. And if it does approach a limit, it may approach different limits according to the manner in which the independent variable approaches its limit. A function is considered to approach a limit only if the same limit is approached regardless of the manner in which the independent variable approaches its limit. If a function approaches different limits then no limit exists.

Important theorems on limits. The following theorems on limits are important:

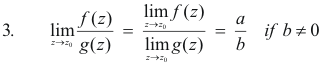
Continuity of a function. Let us consider an arbitrary function w = f(z) and some specific value z₀ of the independent variable. If our function reflects a continuous process, then to values of z which differ only slightly from z₀ there will correspond values of the function f(z) differing only slightly from the value f(z₀) at the point z₀. Thus if the increment z - z₀ of the independent variable is small, then the corresponding increment f(z) - f(z₀) of the function will also be small. We are thus led to the following definition for the continuity of a function at a point:

Def. Continuity at a point. A function f(z) is said to be continuous at a point z = z₀ if f(z₀) is defined and if

Def. Discontinuity. A point in the z-plane where a function f(z) fails to be continuous.

Removable discontinuity. If exists and is not equal to f(z₀), we have what is called a removable discontinuity. By redefining f(z₀) to be the same as the function f(z) becomes continuous at f(z₀).

Continuity in a region. A function f(z) is said to be continuous in a region if it is continuous at all points of the region.

Addition, subtraction, multiplication and division of continuous functions. If continuous functions are added, subtracted, multiplied, or divided (with the exception of division by zero), the result is a continuous function. Division by zero generally produces a discontinuity. Thus in the function

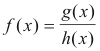
f(x) will generally have a discontinuity at values of x at which h(x) = 0.

Theorems on continuity

Theorem 1. The following functions are continuous in every finite region:

● all polynomials

● e^z

● sin z, cos z

Theorem 2. A continuous function of a continuous function is continuous. More rigorously, if w = f(z) is continuous at z = z₀ and z = g(t) is continuous at t = t₀ where z₀ = g(t₀), then w = f(g(t)) is continuous at t = t₀.

Theorem 3. If a function f(z) is continuous in a closed region, it is bounded in the region. That is, there exists a constant M such that |f(z)| < M for all points z in the region.

Theorem 4. If a function f(z) is continuous in a region, then the real and imaginary parts of f(z) are also continuous in the region.

Uniform continuity. Let f(z) be continuous in a region. By the definition of continuity, at each point z₀ of the region and for any ε > 0 (no matter how small), we can find δ > 0 (which will generally depend on both ε and the particular point z₀) such that |f(z) - f(z₀)| < ε whenever |z - z₀| < δ. If we can find δ depending on ε but not on the particular point z₀, we say that f(z) is uniformly continuous in the region.

Alternatively, f(z) is uniformly continuous in a region if for any ε > 0 we can find δ > 0 such that |f(z₁) - f(z₂)| < ε whenever |z₁ - z₂| < δ where z₁ and z₂ are any two points of the region.

Theorem. If f(z) is continuous in a closed region, it is uniformly continuous there.

Spiegel. Complex Variables (Schaum). pp. 38 - 40

References

Mathematics, Its Content, Methods and Meaning

James and James. Mathematics Dictionary

Spiegel. Complex Variables (Schaum)