Number systems. Rational, irrational, real and complex numbers. Open and closed intervals. Fields. Absolute values, conjugates of complex numbers. Laws

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Number systems. Rational, irrational, real and complex numbers. Open and closed intervals. Fields. Absolute values, conjugates of complex numbers. Laws.

Some numbers such as π, and e are not representable as the quotient of two integers. Thus they lie outside the system of rational numbers. These numbers are called irrational numbers. See the following:

Origin of the Concept of Irrational Numbers

The real number system. The real number system consists of the rational numbers and the irrational numbers. The set of all rational numbers plus the set of all irrational numbers gives the set of all real numbers. The real numbers correspond to points on a line (called the real-number axis), with a one-to-one correspondence between the real numbers and points on the line.

Def. Rational number. A rational number is any number that can be expressed as the quotient of two integers. Thus the set of all rational numbers corresponds to the set of all quotients p/q where p and q are integers.

The following laws hold for rational numbers:

The a/b representation of a rational number is a notation. The quotient a/b can be viewed as simply the number pair (a, b). The rational numbers can then be defined as the set of all ordered pairs (a, b) for which a and b are integers (b ≠ 0) with equality, addition, and multiplication defined as

where 4], 5], 6] are simply 1], 2], and 3] in the new representation.

Irrational number. An irrational number is a number corresponding to any point on the real-number axis that is not representable by the quotient of two integers i.e. it is a number not expressible as the quotient of two integers. Examples: π, and e. The irrational numbers are in fact precisely those infinite decimals which are not repeating. There are two types of irrationals, algebraic and transcendental.

Def. Interval of real numbers. An interval of real numbers is the set containing all numbers between two specified numbers (the end points of the interval ) and one, both, or neither end point. Example: The set of all values of x such that 5 x < 8 is an interval denoted by [5, 8). An interval that contains both of its end points is called a closed interval and is denoted by [a, b], where a and b are the end points. One that contains neither of its end points is called an open interval and is denoted by (a, b).

Concept of a complex number. The concept of a complex number arose out of a circumstance arising in the solution of quadratic equations i.e. equations of type

The solution to this quadratic equation is given by the quadratic formula

Because of the ± sign, this formula would appear to give us two roots for any quadratic equation. However, if the quantity under the radical, b² - 4ac, is negative we realize we have a problem. A negative number has no square root in the system of real numbers i.e. there is no real number which, on being squared, will give a negative number. Thus although the formula gives us an apparent solution when the quantity under the radical is negative, it is an illusion, a false solution. No solution actually exists. One could just leave the matter there. However, mathematicians, in playing around, discovered something interesting. The quantity , where p is a positive number, does not exist, has no intuitive meaning, but if you write it as and then pretend that actually does exist (and denote it by “i”, standing for “imaginary number”) and operate with it by the usual rules of algebra you can test these “false solutions” by plugging them into the original quadratic and you find that they do satisfy the equation. Moreover, you can create an entirely new system of numbers using this newly created “number” i. That system is the one we now call the complex number system. This new system has the real number system embedded in it in the same way that the real number system has the rational number system embedded in it and the rational number system has the system of integers embedded in it. We operate in it using the same algebraic rules that we use for real numbers. Complex numbers have the defect of lacking, generally, a natural intuitive interpretation in the way that the integers, rationals and real numbers do but have been found to be very useful in problems in physics and elsewhere.

Def. Complex number. Any number of the form a + bi, where a and b are real numbers and i² = -1. If z = a + bi, a is called the real part of z, denoted by Re{z}, and b is called the imaginary part of z, denoted by Im{z}. A number such as 3i, where the real part is 0, is called a pure imaginary number.

Syn. Imaginary number

Two complex numbers a + bi and c + di are defined to be equal if and only if a = c and b = d.

If the imaginary part of a complex number is 0, as in 5 + 0i, then the number corresponds to a real number. Thus we can consider the complex number system as having embedded within it, as a subset the real number system.

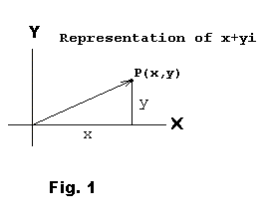
Representation of complex numbers. A complex number x + yi can be identified with a point P(x, y) in the xy plane and viewed as either the point P(x, y) or a vector extending from the origin to P(x, y). See Fig. 1. In this representation the xy plane is called the complex plane. The x axis is the real axis and the y axis is the imaginary axis.

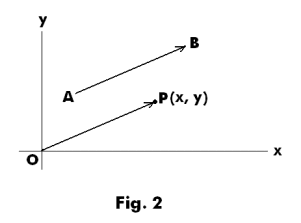
Vector representation of complex numbers. A complex number z = x + iy can be viewed as a vector OP extending from the origin O to the point P(x, y) as shown in Fig. 2. The vector OP is referred to as the position vector of point P. Two vectors having the same length and direction but different initial points, such as OP and AB in the figure, are considered equal. Thus a single complex number corresponding to vector OP also represents any vector in the plane of the same length and direction.

Addition and subtraction of vectors. The sum of two vectors A and B is the vector C as shown in Fig. 3a. We place the initial point of B at the tip of A and C is the vector running from the initial point of A to the tip of B. We write C = A + B.

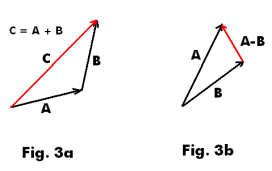
The difference (A - B) of two vectors A and B is the sum of A and (-B) i.e. A - B = A + (-B). The vector A - B is the vector running from the tip of B to the tip of A. See Fig. 3b. We see from the figure that B + (A - B) = A.

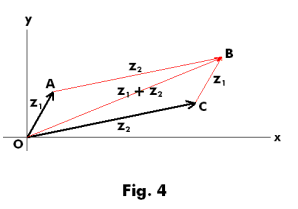
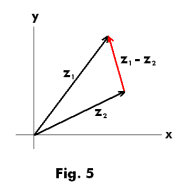
Addition and subtraction of complex numbers. The addition and subtraction of complex numbers corresponds to the laws for the addition and subtraction of vectors. Addition of complex numbers by the usual arithmetic method gives the same result as adding them by the parallelogram law for the addition of vectors. Thus to add complex numbers z₁ and z₂ by the vector method we complete the parallelogram OABC shown in Fig. 4. The sides OA and OC correspond to z₁ and z₂ and the diagonal OB corresponds to z₁ + z₂. The difference z₁ - z₂ between two complex numbers z₁ and z₂ can be thought of as their vector difference which is the vector running from the tip of z₂ to the tip of z₁. See Fig. 5.

Arithmetic operations with complex numbers. The following arithmetic laws hold for complex numbers:

1] (a + bi) + (c + di) = (a + c) + (b + d)i

2] (a + bi) - (c + di) = (a - c) + (b - d)i

3] (a + bi)(c + di) = (ac - bd) + (ad + bc) i

The complex number system meets the axiomatic requirements of an abstract structure called a field.

******************************************

FIELDS

*****************************

Field. A set with two binary operations called addition and multiplication with the following abstract properties:

Addition.

1. Closed under addition.

a,b in S implies a + b in S

2. Associative Law holds under addition.

a + (b + c) = (a + b) + c

3. Identity element called 0 exists under addition.

a + 0 = 0 + a = a for all a in S

4. Inverse exists for every element under addition.

a + (-a) = (-a ) + a = 0 for all a in S

5. Commutative Law holds under addition.

a + b = b + a

Multiplication.

6. Closed under multiplication.

a,b in S implies ab in S

7. Associative Law holds under multiplication.

a(bc) = (ab)c

8. Identity element called 1 (i.e. unit element) exists under multiplication.

1a = a1 = a for all a in S

9. Inverse exists for every nonzero element under multiplication.

aa^-1 = a^-1a = 1 for all a in S (except element 0 is excluded)

10. Commutative Law holds under multiplication.

ab = ba

11. Left Distributive Law holds -- multiplication over addition

a(b+c) = ab + ac

12. Right Distributive Law holds -- multiplication over addition

(a+b)c = ac + bc

13. No proper divisors of zero (i.e. there are no nonzero members a and b for

which ab = 0).

14. Cancellation Law under multiplication holds.

ax = bx implies a = b

Examples of fields: The set of all rational numbers, the set of all real numbers, and the set of all complex numbers.

*************************************************************

Technical definition. Complex number system. The system of complex numbers is the set of ordered pairs (a, b) of real numbers in which

1] (a, b) = (c, d) if and only if a = c and b = d

2] (a, b) + (c, d) = (a + c, b + d)

3] (a, b)(c, d) = (ac - bd, ad + bc)

A noteworthy consequence of this definition is :

(0, 1)(0, 1) = (-1, 0)

(0, -1)(0, -1) = (-1, 0)

That is, the number (-1, 0), i.e. -1, has two square roots (0, 1) and (0,-1) i.e. i and -i.

From this definition one can prove that the complex numbers have all the axiomatic properties listed above for a field.

Conjugate of a complex number. The conjugate of the complex number z = a + bi is a - bi . Two numbers of the type a + bi and a - bi, where a and b are real, are called conjugate complex numbers. We denote the conjugate of a complex number z by . The conjugate of a complex number is also called the complex conjugate.

Example. The numbers 5 + 2i and 5 - 2i are conjugates.

A real number is its own conjugate.

Absolute value of a complex number. The absolute value |z| of the complex number z = a + bi is given by

A complex number a + bi = 0 if and only if a = b = 0.

Laws and properties. If z₁, z₂, ... ,z_n are complex numbers then the following laws hold:

1] | z₁z₂ | = |z₁||z₂| or |z₁z₂ ... z_n | = |z₁||z₂| ..... |z_n|

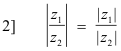
5] The conjugate of the conjugate of a complex number is the number itself:

6] The conjugate of the sum of two complex numbers is the sum of their conjugates:

7] The conjugate of the product of two complex numbers is the product of their conjugates:

References

James and James. Mathematics Dictionary

Spiegel. Complex Variables (Schaum)