Let us suppose that the transformation equations from a rectangular (x, y, z) system to the and systems are given by

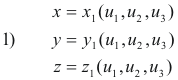
and

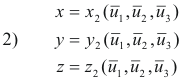
and their inverses

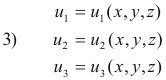
and

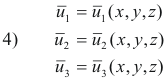
There will exist a transformation directly from the system to the system defined by  

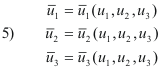
and conversely.

From 5) we obtain

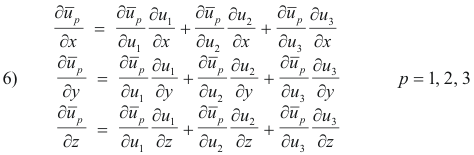
By the definition of a gradient we have

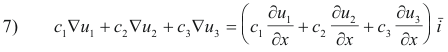
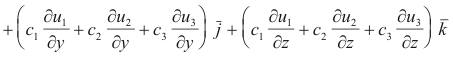
and

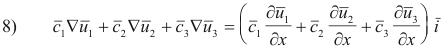
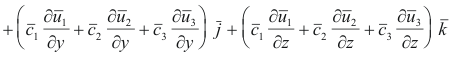
Now the vector A is represented in the two coordinate systems as

The left members of 7) and 8) are thus equal. We now equate the coefficients of in 7) and 8) to obtain

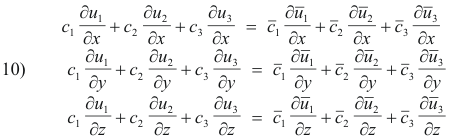
Substituting equations 6) with p = 1, 2, 3 in any of the equations 10) and equating coefficients of

 on each side, we obtain

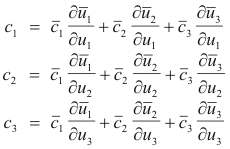
End of proof.