Let us suppose that the transformation equations from a rectangular (x, y, z) system to the and systems are given by

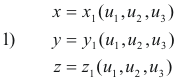
and

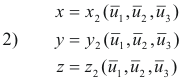
Then there will exist a transformation directly from the system to the system defined by  

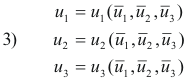
and conversely.

The radius vector to point P is

in the system and

in the system.

From 4) we get

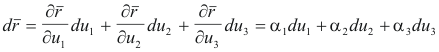
and from 5)

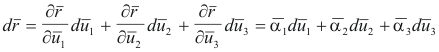
Then

From 3) above we obtain

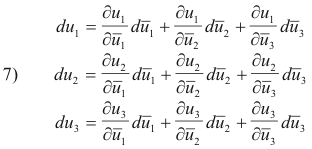
Substituting 7) into 6) and equating coefficients of on both sides we obtain

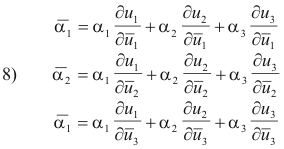
The vector A is given by

and

where C₁, C₂, C₃ and are the contravariant components of A in the two systems.

Substituting 8) into 10) we get

Equating the coefficients of in 9) and 11) we get

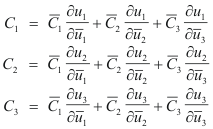
End of proof.