Sequence, limit, accumulation point. Upper, lower bound. Limit superior, inferior. Cauchy sequence. Condition for convergence. Monotonic sequence

SolitaryRoad.com

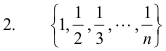
Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

SEQUENCE, CONVERGENCE, LIMIT, ACCUMULATION POINT, BOUND

Def. Sequence. A sequence is a set of numbers, quantities or elements arranged in a definite order. The numbers (or elements) of a sequence are called terms.

Examples of sequences.

1. 2, 4, 6, 8, 10, ..., 2n, ... .

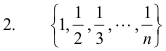
3. {x, 2x², 3x³, ... , nxⁿ}

6. 1, 0, 1, 0, 1, 0, ...

7. any progression (arithmetic, geometric, harmonic)

8. the terms of a series

9. the partial sums of a series

A sequence can be either finite or infinite. An infinite sequence is non-terminating, there being another term after each term. A finite sequence has only a definite number of terms. The i-th term of a sequence is often denoted by a(i) or a_i. Sequences are denoted by notations such as {a₁, a₂, a₃, .... , a_n, .... }, {a_n}, (a_n). A sequence can be viewed as a particular kind of function, a function whose independent variable n ranges over the set of positive integers.

Q. The elements of a sequence can be what? We speak of sequences of numbers (integers, rational numbers, real numbers, etc.). Can the elements of a sequence be anything besides numbers?

A. They can also be

• complex numbers

• points in the plane

• points in 3-space

• points in n-space

• functions

Limit of a sequence. A sequence of numbers {s₁, s₂, s₃, ... , s_n, ... } has the limit s if, for any prescribed accuracy, there is a position in the sequence such that all terms after this position approximate s within this prescribed accuracy i.e for any ε > 0 there exists an N such that |s - s_n| < ε for all n greater than N. A series of points {p₁, p₂, p₃, ... } has the limit p if, for each neighborhood U of p there is a number N such that p_n is in U if n > N.

James and James. Mathematics Dictionary

Example 1. The sequence

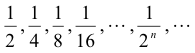
has a limit of 0. The n-th term approaches 0 and meets the requirement of the definition.

Theorem 1. If a sequence has a limit, the limit is unique.

Def. Convergent sequence. A sequence that has a limit is said to be convergent. Otherwise, it is said to be divergent.

Theorem 2. A sequence of numbers {s₁, s₂, .... } is convergent if and only if the series

s₁ + (s₂ - s₁) + (s₃ - s₂) + ... + (s_n - s_n-1) + ...

has a sum.

Bound to a sequence. An upper bound to a sequence of real numbers is a number which is equal to or greater than every number in the sequence. A lower bound to a sequence of real numbers is a number which is equal to or less than every number in the sequence. If a sequence has both an upper bound and a lower bound, it is said to be a bounded sequence. The smallest upper bound is called the least upper bound (lub). The largest lower bound is called the greatest lower bound (glb).

James and James. Mathematics Dictionary

Example 2. The sequence S₁

S₁ = {2 + 1/n | n = 1, ∞} = {3, 2½, 2⅓, 2¼, ...}

consists of a sequence of numbers that approaches 2 from the right side but never reaches 2. A lower bound for this set of numbers is the number 2 or any number less than 2, (such as the numbers 1, 0.5, -6, etc. ). The greatest lower bound (glb) of this set is 2. Unlike the situation for a finite set of numbers where there will always be some smallest number in the set, in an infinite set there may not be any smallest number but there may be a greatest lower bound that plays a role similar to that of the smallest number of the set. An upper bound for this set S₁ is the number 3 or any number larger than 3. In general, when talking about greatest lower bounds and least upper bounds, there is an infinite number of numbers that qualify. The least upper bound of this set is the number 3. Consider the sequence S₂

S₂ = {2 + 1/n, 6 - 1/n | n = 1, ∞} = {3, 5, 2½, 5½, 2⅓, 5⅔, 2¼, 5¾, ...}

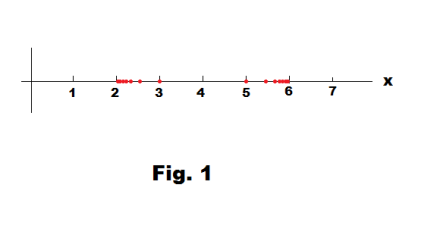
This really is two sequences of numbers, one approaching 2 from the right and the other approaching 6 from the left as shown graphically in Fig. 1. The greatest lower bound of this set is 2 and the least upper bound is 6.

Def. Accumulation point (or cluster point or limit point) of a sequence. A point P such that there are an infinite number of terms of the sequence in any neighborhood of P.

Example 3. The sequence

has two accumulation points, the numbers 0 and 1. The sequence S₁

S₁ = {2 + 1/n | n = 1, ∞} = {3, 2½, 2⅓, 2¼, ...}

has a cluster point (or accumulation point) at the value 2. The sequence S₂

S₂ = {2 + 1/n, 6 - 1/n | n = 1, ∞} = {3, 5, 2½, 5½, 2⅓, 5⅔, 2¼, 5¾, ...}

has a cluster point (or accumulation point) at the values 2 and 6.

Limit superior. For a sequence of real numbers, the largest accumulation point is called the limit superior and denoted by lim sup or . It corresponds to the cluster point farthest to the right on the real line. A number is called the limit superior if infinitely many terms of the sequence are greater than - ε for any positive ε, while only a finite number of terms are greater than + ε.

Syn. greatest limit, maximum limit, upper limit

Limit inferior. For a sequence of real numbers, the smallest accumulation point is called the limit inferior and denoted by lim inf or . It corresponds to the cluster point farthest to the left on the real line. A number l is called the limit inferior if infinitely many terms of the sequence are less than l + ε for any positive ε, while only a finite number of terms are less than l - ε.

Syn. least limit, minimum limit, lower limit

Example 4. In the sequence S₂

S₂ = {2 + 1/n, 6 - 1/n | n = 1, ∞} = {3, 5, 2½, 5½, 2⅓, 5⅔, 2¼, 5¾, ...}

the limit superior is 6 and the limit inferior is 2.

In the sequence S₃

S₃ = {2 + 1/n, 6 - 1/n, 10 + 1/2n | n = 1, ∞}

the limit superior is 10 and the limit inferior is 2. The cluster point farthest to the right is at 10 and the one farthest to the left is at 2. The greatest lower bound of the sequence is 2 and the least upper bound is 10½.

Cauchy’s condition for convergence of a sequence. An infinite sequence converges if, and only if, the numerical difference between every two of its terms is as small as desired, provided both terms are sufficiently far out in the sequence. Tech. The infinite sequence s₁, s₂, s₃, ... , s_n, ... converges if, and only if, for every ε > 0 there exists an N such

| s_n+h - s_n | < ε

that for all n > N and all h > 0.

James and James. Mathematics Dictionary

Def. Cauchy sequence. A Cauchy sequence is a sequence where, given any preassigned positive number ε, however small, there exists a point in the sequence (possibly very far out) beyond which the distance between any two selected elements is less than ε. Tech. A Cauchy sequence is a sequence of points P₁, P₂, ... such that for any ε > 0 there is a number N for which ρ(P_i, P_j) < ε if i > N and j > N, where ρ(P_i, P_j) is the distance between P_i and P_j. If the points are points of Euclidean space, this is equivalent to the sequence being convergent. If the points are real (or complex) numbers, then ρ(P_i, P_j) is | P_i - P_j | and the sequence is convergent if and only if it is a Cauchy sequence.

Syn. Convergent sequence, fundamental sequence, regular sequence.

James and James. Mathematics Dictionary

Monotonic sequences.

Monotonic increasing sequence. A sequence of real terms a₁, a₂, ... ,a_n, ... such that a_n+1 ≥a_n for all n i.e. a sequence in which the terms either increase or remain the same.

Monotonic decreasing sequence. A sequence of real terms a₁, a₂, ... ,a_n, ... such that a_n+1≤a_n for all n i.e. a sequence in which the terms either decrease or remain the same.

Theorem. Every monotonic (increasing or decreasing) sequence a₁, a₂, ... ,a_n, ... with the property that |a_n| < M (a constant) converges. That is, every bounded monotonic sequence has a limit.

Theorems on limits of sequences. For sequences consisting of numbers the following hold:

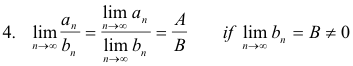
References.

James and James. Mathematics Dictionary.

Taylor. Advanced Calculus.

Spiegel. Advanced Calculus. (Schaum)