Conics. Ellipse, hyperbola, parabola, circle

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

CONICS. ELLIPSE, HYPERBOLA, PARABOLA, CIRCLE

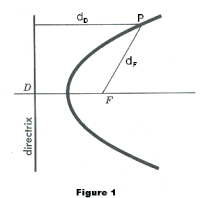
Conic. A conic is any curve which is the locus of a point which moves in such a way that the ratio of its distance from a fixed point to its distance from a fixed line is constant. The ratio is the eccentricity of the curve, the fixed point is the focus, and the fixed line is the directrix. See Figure 1. The eccentricity is always denoted by e. Referring to Figure 1,

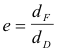
where d_F is the distance of point P from the focus F and d_D is its distance from the directrix. When e = 1, the conic is a parabola; when e < 1 it is an ellipse; when e > 1, it is a hyperbola.

Conics as cross sections of a circular cone. Conics are given by the intersection of a plane with a circular cone. The intersection will correspond to one of the conic curves (ellipse, hyperbola, parabola, etc.) depending on the angle at which the plane cuts the cone. See Figure 2. Because of this, conics are also called conic sections. Let φ be the acute angle that the intersecting plane makes with the axis of the cone and let α be the acute angle that the generator of the cone makes with the axis of the cone. Then

Value of φ	Conic section created
φ = 90^o	circle
α < φ < 90^o	ellipse
φ = α	parabola
φ < α	hyperbola

DEFINITIONS.

Chord of a curve. A line segment joining any two distinct points on the curve.

Focal chord of a conic. A chord passing through a focus of the conic.

Focal radius of a conic. A line segment joining a focus to a point on the conic.

Principal axis of a conic. The line passing through the focus perpendicular to the directrix.

Latus rectum of a conic. The chord passing through the focus parallel to the directrix.

Vertex of a conic. A point where the conic crosses the principal axis.

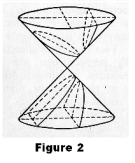
Referring to Figure 3, DF is the principal axis, V is the vertex, BB' is a focal chord, FB is a focal radius, and LL' is the latus rectum.

***************************

THE PARABOLA

***************************

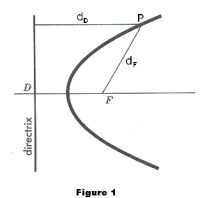
Parabola. A parabola is the locus of a point which moves in a plane in such a way that its distance from a fixed point of the plane and from a fixed line of the plane are equal. Referring to Figure 1, a parabola is the locus of point P moving in such a way that always

d_F = d_D

where d_F is its distance from the focus and d_D is its distance rom the directrix.

Stated differently, a parabola is the set of all points in the plane that are equidistant from a fixed point and a fixed line in the plane.

Standard form of the parabola. The equation of a parabola assumes its simplest form (i.e. its reduced canonical form) when its vertex is at the origin and its axis coincides with one of the coordinate axes.

Axis coincides with the x axis. When the vertex is at the origin and the axis coincides with the x-axis, the equation of the parabola is

1) y² = 4px

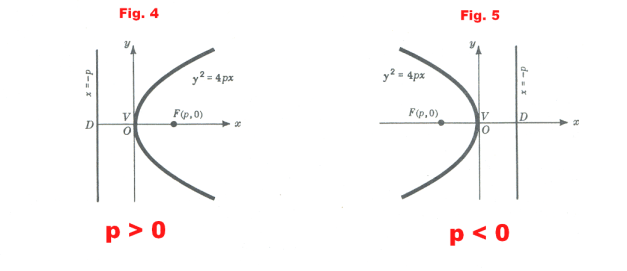
In this form the focus is at F(p, 0) and the equation of the directrix is x = - p. If p > 0, the parabola opens to the right. See Figure 4. If p < 0 , the parabola opens to the left. See Figure 5.

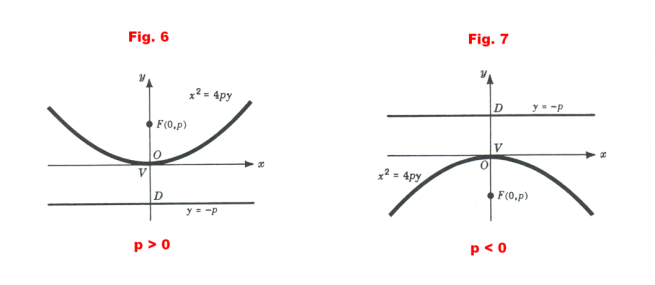
Axis coincides with the y axis. When the vertex is at the origin and the axis coincides with the y axis, the equation of the parabola is

2) x² = 4py

In this form the focus is at F(0, p) and the equation of the directrix is y = - p. If p > 0, the parabola opens upward. See Figure 6. If p < 0 , the parabola opens downward. See Figure 7.

Note. Some authors use a different convention in regard to the standard form of the parabola. Some authors give the standard form as y² = 2px, in which case the focus is at (½ p, 0) and the directrix is located at x = - ½ p.

**********************

THE ELLIPSE

**********************

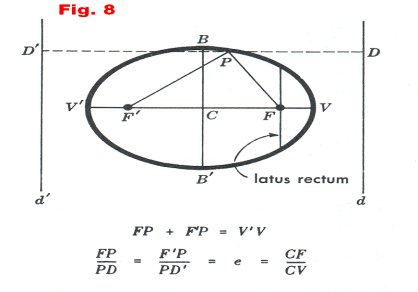
Ellipse. An ellipse is a figure formed by a point which moves in the plane in such a way that the sum of its distances from two fixed points is constant. See Figure 8. The ellipse is the locus of point P moving in such a way that always

where q is a constant. The constant q is equal to the distance V'V (the length of the major axis).

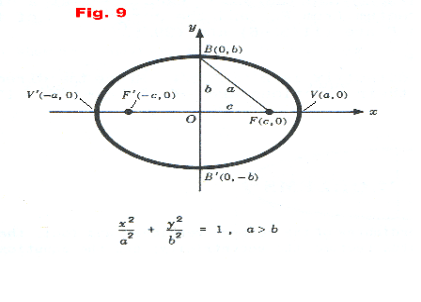
Definitions, terms. The fixed points F and F' in Figure 8 are called the foci and the point C midway between them is called the center. The points V and V' are the vertices, the segment V' V is called the major axis, the segment B'B is called the minor axis, the line segment CV is called the semimajor axis and the line segment CB is called the semiminor axis. The principal axis is the major axis.

Equivalent definition of an ellipse. An equivalent definition of an ellipse is that it is the locus of a point P which moves in such a way that the ratio of its distance from a fixed point F to its distance from a fixed line D is a constant e < 1, called the eccentricity. In Figure 8, the fixed point is the focus F or F' and the fixed line is the directrix d or d'. The ratio FP/PD = F'P/PD' = e is the eccentricity. It can be shown that the eccentricity e is also equal to the ratio CF/CV.

We can take as a definition of an ellipse any property that defines it. An ellipse can also be defined as the result of a “uniform contraction” of a circle toward one of its diameters, a definition equivalent to the above.

Standard form of the ellipse. The equation of an ellipse assumes its simplest form (i.e. its reduced canonical form) when its center is at the origin and its principal axis coincides with one of the coordinate axes. Let a and b represent the lengths of the semimajor and semiminor axes, respectively. Then the standard form of the equation of an ellipse is either

according to whether the principal axis lies on the x axis or the y axis.

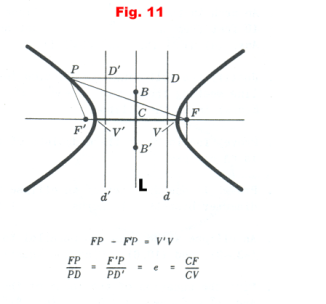
Principal axis is the x axis. When the center is at the origin and the principal axis is the x axis, the equation of the ellipse is

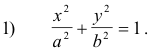
See Figure 9. The vertices are at V(a, 0) and V'(-a, 0). The length of the major axis is V'V = 2a and the length of the minor axis is B'B = 2b. The foci are on the major axis at F(c, 0) and F(-c, 0) where

Principal axis is the y axis. When the center is at the origin and the principal axis is the y axis, the equation of the ellipse is

See Figure 10. The vertices are at V(0, a) and V'(0, -a). The length of the major axis is V'V = 2a and the length of the minor axis is B'B = 2b. The foci are on the major axis at F(0, c) and F(0, -c) where

In both cases, the length of a latus rectum is 2b²/a, the eccentricity is

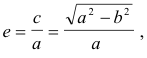
and the directrices are perpendicular to the major axis at distances a²/c or a/e from the center.

******************************

THE HYPERBOLA

******************************

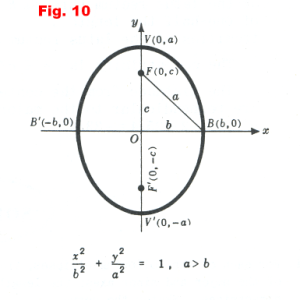
Hyperbola. A hyperbola is the locus of a point which moves in the plane in such a way that the absolute value of the difference of its distances from two fixed points in the plane is constant. Referring to Figure 11, the hyperbola is the locus of point P moving in such a way that always

| FP - F'P | = q

where q is a constant. Referring to Fig. 11, q is equal to the distance V'V.

Definitions, terms. The fixed points F and F' in Figure 11 are called the foci and the point C midway between them is called the center. The points V and V' are the vertices. The segment V' V is called the transverse axis. The principal axis is the transverse axis. Let L be a line passing through C perpendicular to F'F. Then a certain line segment BB' defined on line L, having C as midpoint, is called the conjugate axis.

A hyperbola can also be defined as the locus of a point which moves in such a way that the ratio of its distance from a fixed point to its distance from a fixed line is a constant greater than one.

This definition gives only a single branch of the hyperbola. In Figure 11, the fixed point is the focus F (or F') and the fixed line is directrix d (or d'). The ratio is the eccentricity, e. The other branch is given by the conjugate focus and directrix.

Standard form of a hyperbola. The equation of a hyperbola assumes it simplest form (i.e. its reduced canonical form) when its center is at the origin and its axis coincides with one of the coordinate axes.

Principal axis is the x axis. When the center is at the origin and the principal axis is the x axis, the equation of the hyperbola is

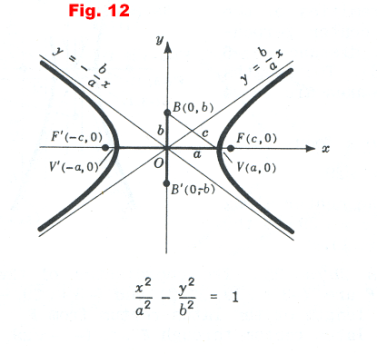
See Figure 12. The vertices are at V(a, 0) and V'(-a, 0). The length of the transverse axis is V'V = 2a. The extremities of the conjugate axis are B'(0, -b) and B(0, b) and its length is B'B = 2b. The foci are on the transverse axis at F(c,0) and F(-c, 0) where

Principal axis is the y axis. When the center is at the origin and the principal axis is the y axis, the equation of the hyperbola is

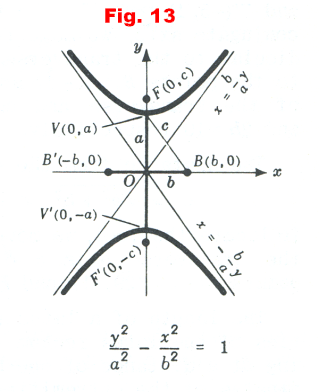
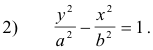
See Figure 13. The vertices are at V(0, a) and V'(0, -a). The length of the transverse axis is V'V = 2a.. The extremities of the conjugate axis are B'(-b, 0) and B(b, 0) and its length is B'B = 2b. The foci are on the major axis at F(0, c) and F(0, -c) where

In both cases, the length of a latus rectum is 2b²/a, the eccentricity is

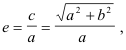
and the directrices are perpendicular to the major axis at distances a²/c or a/e from the center.

Asymptotes of a hyperbola. The straight lines

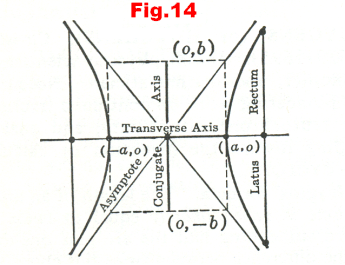
are called the asymptotes of the hyperbola 1). See Figure 13. The asymptotes pass through the corners of a rectangle defined by the lines x = a, x = -a, y = b, y = -b. See Figure 14. A convenient way to draw a hyperbola is to draw the rectangle, then draw the asymptotes through the corners, and then draw the hyperbola. The vertices are at the points where the sides of the rectangle cross the x axis. The foci are at a distance from the origin equal to one-half the diagonal of the rectangle.

The asymptotes of the hyperbola 2) are given by

In this case the rectangle is defined by the lines y = a, y = -a, x = b, x = -b.

The asymptotes have the property that the perpendicular distance from a point on a hyperbola to an asymptote approaches zero as the point moves indefinitely far from the center.

Def. Rectangular hyperbola. A hyperbola whose major and minor axes are equal. Its equation, in standard form, is x² - y² = a². The equations of the asymptotes are y = x and y = -x.

Syn. equiangular hyperbola, equilateral hyperbola.

Def. Conjugate hyperbolas. Two hyperbolas such that the transverse axis of each is the conjugate axis of the other. The two hyperbolas

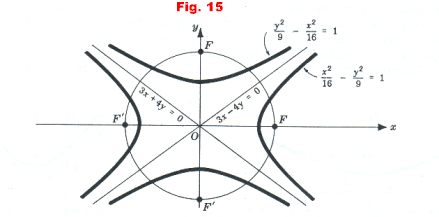
are conjugate hyperbolas. See Figure 15.

A pair of conjugate hyperbolas have the same center and the same asymptotes. Their foci lie on a common circle as shown in the figure.

************************************************************

Polar form of the equation of a conic. Let the focus of a conic be at the pole of a polar coordinate system and let the directrix be perpendicular to the polar axis and at a distance q to the left of the pole. Let e be the eccentricity. Then the equation of the conic in polar form is

If the directrix is located at a distance q to the right of the pole the equation is

Properties of Conics.

Parabola. A ray of light issuing from its focus is reflected by the parabola parallel to the axis of symmetry of the parabola. Applications: automobile headlight, search light, reflecting telescope.

Ellipse. A ray of light issuing from one of its foci and reflected by the ellipse passes through the other focus.

Hyperbola. A ray of light issuing from one of its foci is reflected by the hyperbola as if it originated from the other focus.

******************************

THE CIRCLE

******************************

Circle. A circle is a special case of an ellipse.

Circle - Standard form. The standard form of an equation of a circle centered at point (h, k) with radius r is

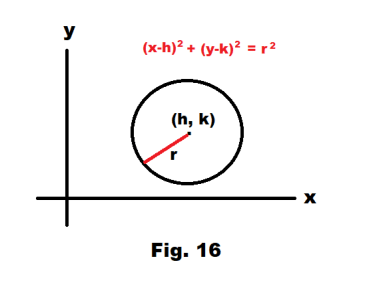
(x - h)² + (y - k)² = r²

See Fig. 16.

Circle - General form.

Ax² + Ay² + Dx + Ey + F = 0, A ≠ 0

x² + y² + 2dx + 2ey + f = 0

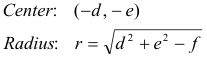
Circle on line segment P₁P₂ as diameter.

(x - x₁)(x - x₂) + (y - y₁)(y - y₂) = 0

where P₁(x₁, y₁) and P₂(x₂, y₂) are the end points of a diameter.

Three point form. If a circle passes through the three points P₁(x₁, y₁), P₂(x₂, y₂), and P₃(x₃, y₃), its equation is given by

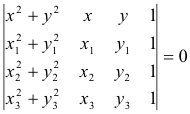
References.

Ayres. First Year College Mathematics. Chap. 52 - 54.

James and James. Mathematics Dictionary.