Website owner: James Miller
BASIC CONCEPTS, LOCUS, SOLUTION SET, COORDINATE SYSTEMS, SLOPES, ANGLES, POINT OF DIVISION, INTERCEPTS
*******************
BASIC CONCEPTS
*******************
The basic idea of analytic geometry is that idea originated by Rene Descartes in the 1600's of representing an equation in two variables,
f(x, y) = 0,
graphically in a rectangular coordinate system. He introduced the ideas of a rectangular coordinate system and the coordinate representation of a point. Before his day there was no graphical means available for viewing an equation. People focused on solving equations in a single variable for the unknown, viewed everything totally algebraically, and an equation in two variables was viewed as indeterminate and uninteresting. An idea central to analytic geometry is that of a locus of an equation. The locus of an equation is the totality of all points whose coordinates satisfy the equation. The locus of an equation is the solution set of the equation, the solution set being the set of all solutions of the equation. We plot the solution set of an equation in a coordinate system to give ourselves a pictorial representation of the locus.
Def. Solution set. The set of all solutions of a given equation, system of equations, inequality, etc. E.g. the solution set of the equation x2 - 2x = 0 is the set whose members are the numbers 0 and 2; the solution set of x2 + y2 = 4 is that set of coordinates (x, y) that satisfy the equation, corresponding in this case to a circle with center at the origin and radius 2; the solution set of the system, x + y = 1, x - y = 3, is the set whose only member is the ordered pair (2, -1); the solution set of the inequality 3x + 4y + z < 2 is the set of all ordered triplets (x, y, z) that represent points which are below the plane whose graph is 3x + 4y + z = 2 .
James and James. Mathematics Dictionary.
Def. Locus. Any system of points, lines, or curves which satisfies one or more given conditions. If a set of points consists of those points (and only those points) whose coordinates satisfy a given equation, then the set of points is the locus of the equation and the equation is the equation of the locus. E.g. the locus of the equation 2x + 3y = 6 is a straight line, the line which contains the points (0, 2) and (3, 0). The locus of points which satisfy a given condition is the set which contains all the points which satisfy the condition and none which do not; e.g. the locus of points equidistant from two parallel lines is a line parallel to the two lines and midway between them; the locus of points at a given distance r from a given point P is the circle of radius r with center art P.
James and James. Mathematics Dictionary.
Two fundamental problems of analytic geometry. Two fundamental problems of analytic geometry are:
1] Given an equation, to find the locus.
2] Given a locus defined by some geometrical condition, to find the corresponding equation. [For example, a problem such as: Find the equation of the locus of a point which is equidistant from the points (-2, 3) and (5, 8)].
Plane analytic geometry. In plane analytic geometry we deal with equations in two variables. Equations in two variables can be classified as:
1] Equations of the first degree in two variables, the general form of which is
ax + by + c = 0
2] Equations of the second degree in two variables, the general form of which is
ax2 + bxy + cy2 + dx + ey + d = 0
3] Equations of degree higher than two in two variables.
Any equation in two variables can be represented as a graph in a rectangular x-y coordinate system.
Fundamental theorems:
Theorem 1. The locus of an equation of the first degree in two variables is a straight line.
Theorem 2. The locus of an equation of the second degree in two variables is a conic (i.e. an ellipse, hyperbola, or parabola).
Note. Conics include some degenerate cases: 1) a point, 2) a straight line and 3) a pair of straight lines.
************************
COORDINATE SYSTEMS
************************
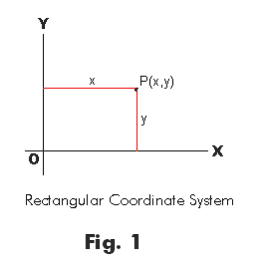
Rectangular Coordinate System. A coordinate system in which the position of a point P(x, y) is given by its distance from each of two lines or axes OX and OY, which are perpendicular to each other. See Fig. 1.

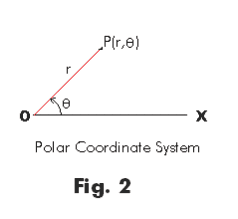
Polar Coordinate System. A coordinate system in which the position of a point P(r, θ) is given by its radial distance r from an origin O and the angle θ measured counterclockwise from a horizontal line OX called the polar axis to line OP. See Fig. 2. The line OP from the origin to the point is called the radius vector, the angle θ is called the polar angle, and the origin O is called the pole.
Transformations between polar and rectangular coordinates. The formulas for converting from rectangular to polar coordinates or vice versa are:
x = r cos θ
y = r sin θ
θ = arc tan y/x
![]()
********************************
POINTS, SLOPES AND ANGLES
********************************
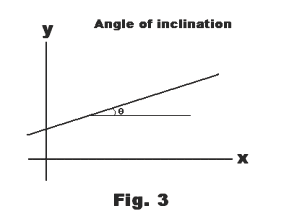
Angle of inclination of a line. The angle (measured counterclockwise) from the positive direction of the x-axis to the line. It is usually taken to be between 0o and 180o. See Fig. 3.
Slope of a line. The tangent of the angle of inclination.
Directed line segment. A line segment extending from some point P1 to another point P2 viewed as having direction associated with it, the positive direction being from P1 to P2. A directed line segment P1P2 corresponds to a vector which extends from point P1 to point P2.
Syn. directed line
Def. Direction angles of a directed line segment. The angles α and β that a line segment P1P2 makes with the positive x and y coordinate directions, respectively, are called the direction angles of the line segment. In other words, if the x-y coordinate system is envisioned as translated to the point P1 of P1P2 the direction angles α and β are the angles that P1P2 makes with the positive x and y axes.
Def. Direction cosines of a directed line segment. The direction cosines of a directed line segment are the cosines of the direction angles of the line segment.
Let two points P1(x1, y1) and P2(x2, y2) define directed line segment P1P2. Then the direction cosines of P1P2 are given by
![]()
where d is the distance between points P1 and P2 (i.e. the length of P1P2 ).
Direction cosines are not independent. When one of them is given, the other can be found, except for sign, from the relation
![]()
We shall denote the direction cosines cos α and cos β of a directed line segment by λ and μ, respectively. Intuitively, the direction cosines λ and μ of a directed line segment (i.e vector) correspond to the projections of its associated unit direction vector on the x and y axes where its associated unit direction vector is a unit vector of the same direction emanating from the origin.
Def. Direction numbers of a directed line segment. Any two numbers proportional to the direction cosines of the line segment.
If λ and μ are direction cosines of a directed line segment P1P2, its direction numbers l, m are given by
l = kλ, m = kμ
where k is any number different from zero. The relationship between direction cosines and direction numbers can also be expressed as
![]()
● If points P1(x1, y1) and P2(x2, y2) define directed line segment P1P2, then the two numbers x2-x1, y2-y1 or any multiple of them, constitute a set of direction numbers for the line segment.
Slope m of line segment P1P2. The slope of the line segment from P1(x1,y1) to P2(x2,y2) is
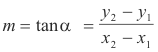
where α is the angle of inclination of P1P2.
Angle θ between two lines of slopes m1 and m2.
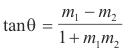
For perpendicular lines: m1m2 = -1
Condition for perpendicularity of two lines. Two lines are perpendicular if m1 = - 1/m2 (slopes) or if λ1λ2 + μ1μ2 = 0 (direction cosines).
Distance d between two points P1(x1,y1) and P2(x2,y2).
![]()
Point of division. The point which divides the line segment joining two given points in a given ratio. If the two given points have the Cartesian coordinates (x1, y1) and (x2, y2) and it is desired to find a point P such that the distance form the first point to the point P, divided by the distance from the point P to the second pont, is equal to r2 /r1, the formulas giving the coordinates x and y of the desired point P are
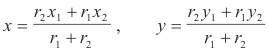
When r1/r2 is positive, the point of division lies between the two given points, and the division is internal; the point divides the line segment internally in the ratio r1/r2. When the ratio is negative, the of division must lie on the line segment extended, and it divides the line segment externally in the ratio | r1/r2 | . When r1 = r2, the point P bisects the line segment and the above formulas reduce to
![]()
For points in space, the situation is the same as in the plane except that the points now have three coordinates. The formulas for x and y are the same, and the formula for z is
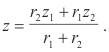
James and James. Mathematics Dictionary
Area of a triangle. The area A of a triangle with vertices given by P1(x1, y1), P2(x2, y2), and P3(x3, y3) is
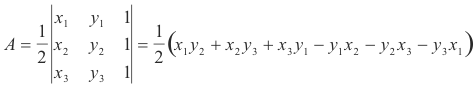
Area of a polygon. The area A of a polygon bounded by the points P1(x1, y1), P2(x2, y2), ..., Pn(xn, yn) is
A = ½ (x1y2 + x2y3 + ... + xn-1 yn + xny1 - y1x2 - y2x3 - ... yn-1xn - ynx1)
The formula can be remembered by the following device:
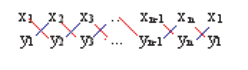
Intercept. The intercept of a straight line, curve, or surface on a coordinate axis is the distance from the origin to the point where the line, curve, or surface cuts the axis. The intercept on the x-axis is the x -intercept, the intercept on the y-axis is the y-intercept, and the intercept on the z-axis is the z-intercept.
Example. The intercepts of the line 2x + 3y = 6 on the x-axis and y-axis, respectively, are 3 and 2.
Theorem. Points P1(x1, y1), P2(x2, y2), and P3(x3, y3) are collinear if and only if
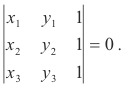
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life