Website owner: James Miller
GENERAL EQUATION OF THE SECOND DEGREE, QUADRIC SURFACES, REDUCTION TO CANONICAL FORM, THE 17 CANONICAL FORMS, TRANSFORMATION OF COORDINATES
General equation of the second degree. The general equation of the second degree in three variables is
1) f(x, y, z) = ax2 + by2 + cz2 + 2fyz + 2gxz + 2hxy + 2px + 2qy + 2rz + d = 0.
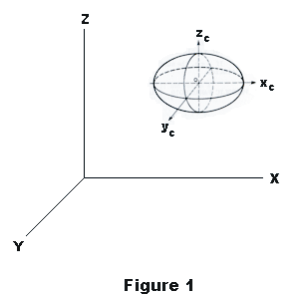
This equation has as its locus a surface in space called a quadric surface or a conicoid. See figure 1. Quadric surfaces consist of ellipsoids, hyperboloids, paraboloids, and certain limiting or degenerate forms of these.

Simplification by a change of coordinate system. The algebraic expression for any curve or surface is dependent on the location and orientation of the coordinate system. When the coordinate system is rotated or moved in any way the expression for the curve or surface changes. The general equation of the second degree can be simplified greatly by a change to a different coordinate system. A suitable rotation of the coordinate system will eliminate all of the mixed terms in xy, xz and yz. A suitable translation will eliminate most or all of the first degree terms in x, y and z. By a suitable translation and rotation of the coordinate system the general second degree equation can be reduced to one of the following canonical forms:


Let us make some observations concerning some of the surfaces.
● An ellipsoid can be conceived of as a surface obtained from a sphere by uniformly stretching (or compressing) the sphere in three mutually perpendicular directions by given amounts. The equation of a sphere centered at the origin is
2) x2 + y2 + z2 = 1
and the equation of an ellipsoid centered at the origin is
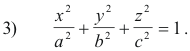
If (x, y, z) is a point satisfying equation 2) then (ax, by, cz) is a point satisfying equation 3). Thus if P (x, y, z) is a point on sphere 2) then P'(ax, by, cz) is the corresponding point on ellipsoid 3).
● The hyperboloid of one sheet (Form 3), hyperboloid of two sheets (Form 4), second-order cone (Form 5), and elliptic paraboloid (Form 7) all appear in special cases as surfaces of revolution. The general forms of these surfaces can be viewed as produced by a uniform stretching of their surface of revolution form in a way similar to the way an ellipsoid can be produced from a sphere by stretching. For example, the equation of the hyperboloid of one sheet is
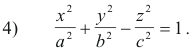
If a = b it is a surface of revolution with equation
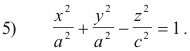
Surface 4) can be obtained from surface 5) by a stretching in the y direction by a coefficient b/a. The same is true of the other surfaces — the hyperboloid of two sheets, second-order cone, etc. We can take the surface in its surface of revolution form and stretch it in a direction perpendicular to its axis, in the x or y direction, to get a general form.
● One can learn a lot about surfaces such as these by examining cross sections. For example, one can examine cross sections perpendicular to the z axis of 5) by setting z = k and see that they are circles. We can also look at a cross section created by a plane passing through (containing) the z axis. For example, if we substitute y = 0 into 5) we get the equation of the intersection of the surface with the plane y = 0. We note that it is a hyperbola. Such curves obtained by passing planes through the axis of revolution are called meridians. A surface of revolution can be obtained by rotating a meridian about the axis of revolution.
● The forms 9 - 17 are all represented by equations in only the two variables x and y (the variable z is missing). They thus all correspond to cylinders whose directrices are the corresponding curves in the x-y plane and whose generators are lines parallel to the z axis.
*******************************************************
TRANSFORMATION OF COORDINATES
*******************************************************
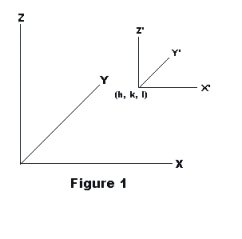
To transform an equation of a surface from an old system of rectangular coordinates (x, y, z) to a new system of rectangular coordinates (x', y', z'), substitute for each old variable in the equation of the surface its expression in terms of the new variables.
Translation of coordinate system. Let the origin of the new x'-y'-z' system be at point (h, k, l) of the old x-y-z system with the axes of the new system parallel to the corresponding axes of the old system. Then
x = x' + h
y = y' + k
z = z' + l
See Figure 1.
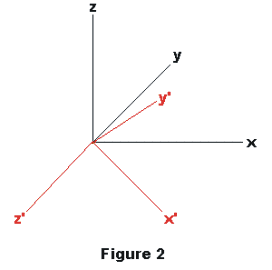
Rotation of the axes about the origin. Let the origin of the new x'-y'-z' system be coincident with the origin of the old system and let λ1, μ1, ν1 be the direction cosines of the x' axis, λ2, μ2, ν2 be the direction cosines of the y' axis, λ3, μ3, ν3 be the direction cosines of the z' axis.
Then
x = λ1x' + λ2y' + λ3z'
1) y = μ1x' + μ2y' + μ3z'
z = ν1x' + ν2y' + ν3z'
x' = λ1x + μ1y + ν1z
2) y' = λ2x + μ2y + ν2z
z' = λ3x + μ3y + ν3z
We can write these equations in matrix form as
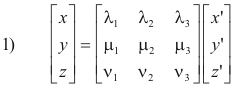
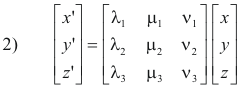
where the matrices are called rotation matrices. Multiplication by a rotation matrix transforms the coordinates of a point from one system to another system.
Note. Equation 1) is best understood in vector terms as a change of basis where 1) is equivalent to
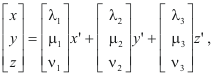
the vectors
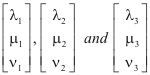
representing orthogonal, unit basis vectors.
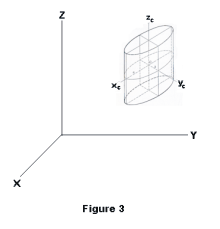
Equations relating the coordinates of the original and canonical coordinate systems of a quadric surface. Let x, y and z be the coordinates of a point P with respect to the original X-Y-Z coordinate system and xc, yc and zc be the coordinates of the point with respect to the canonical Xc-Yc-Zc coordinate system. See Figure 3. Let the origin of the canonical Xc-Yc-Zc system be located at (x0, y0, z0) and let λ1, μ1, ν1 be the direction cosines of the xc axis, λ2, μ2, ν2 be the direction cosines of the yc axis, λ3, μ3, ν3 be the direction cosines of the zc axis with respect to the X-Y-Z coordinate system. Then the relationship between the coordinates x, y, and z and xc, yc and zc is given by the following equations:
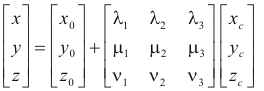
and
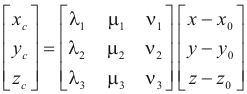
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life