Website owner: James Miller
DOUBLE INTEGRAL, TRIPLE INTEGRAL, ITERATED INTEGRAL

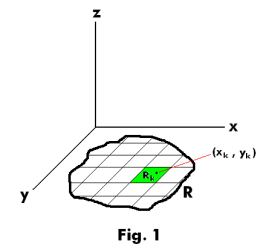
Def. Double integral. Let z = f(x, y) be a function defined and continuous over a finite region R of the xy-plane. Let this region be subdivided into n subregions R1, R2, ... ,Rn of respective areas ΔA1, ΔA2, ... ,ΔAn. See Fig. 1. The manner of subdivision is arbitrary. In each subregion Rk we select a point Pk(xk, yk) and form the sum
![]()
Next we define the diameter ri of a subregion Ri to be the greatest distance between any two points within or on its boundary. The double integral of the function f(x, y) over the region R is then defined as
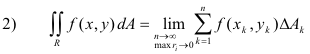
where we stipulate that the maximum ri → 0 as n → 0.
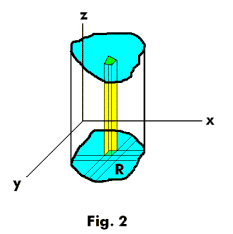
When z = f(x, y) is non-negative over the region R the double integral 2) may be interpreted as a volume. Any term fk(xk, yk)ΔAk of 1) gives the volume of a vertical column standing on ΔAk as a base and of height zk. See Fig. 2. The sum of all these terms gives an approximation to the volume of the cylindrical column standing on a base consisting of the region R, sides generated by a line parallel to the z axis moving along the boundary of R, and top, the cut-off section of surface z = f(x, y).
Thus we see that in exact analogy to the way we defined the definite integral
![]()
as the limit of a sum and interpreted it as an area, we define the double integral as the limit of a sum and interpret it as a volume.
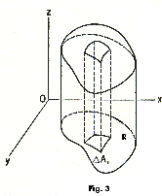
The iterated integral. Consider the function z = f(x, y) defined over a region R as shown in Fig. 3. The double integral of this function over region R is defined by 2) above. We will now demonstrate a method for computing this integral. We know how to find the volume of various solids by the method of slicing. The volume is expressed as the integral
![]()
where A(x) represents the area of a variable cross-section of the solid, all the sections being made by planes perpendicular to a fixed line. We shall now employ this method to evaluate the double integral.
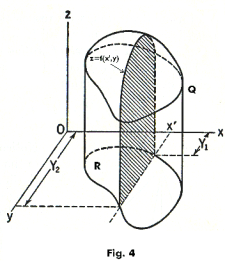
Consider the cylindrical column shown in Fig. 4. Label the cylindrical column “Q”. Let a plane x = x', parallel to the yz-plane, be passed through column Q as shown. The cross-section of column Q created by this plane corresponds to the area under the curve z = f(x', y) between points (x', Y1) and (x', Y2), where (x', Y1) and (x', Y2) are the points where the intersecting plane crosses the boundary of region R. The area of this cross-sectional slice is given by the integral
![]()
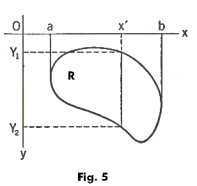
Consider the drawing of region R shown in Fig. 5. Let a be the smallest value which x can have in R, and b the largest value. R is assumed to be a region such that the line x = x', for each value of x' between a and b, cuts the boundary of R just twice, no more. The corresponding values of y are Y1 and Y2, where Y1 < Y2. For a given value of x', the values of Y1 and Y2 can be found from the equations of the boundary of R where y = Y1(x) defines one part of the boundary and y = Y2(x) defines the other part.
Upon dropping the primes, 4) can be written as
![]()
The expression As(x) plays the role of A(x) in formula 3), representing a slice of cylinder Q. Hence the volume V of cylinder Q is given by the integral
![]()
or
![]()
The inner integration, with respect to y, is to be performed first. The result is a function of x, which is then integrated between the limits x = a and x = b. In the first integration x is regarded as a constant.
The expression 5) for V is called an iterated integral. It is usually written as
![]()
we have just shown the technique for evaluating double integrals. They are evaluated by an iterated integral. The relationship between iterated integrals and double integrals is so important that we state it in a theorem:
Theorem 1. The double integral of a continuous function f(x, y) over a region A of the plane can be evaluated by either of the two iterated integrals:
![]()
![]()
where the limits of integration are determined with reference to the boundary of area A.
Def. Iterated integral. An indicated succession of integrals in which integration is to be performed first with respect of one variable, the others being held constant, then with respect to a second, the remaining ones being held constant, etc.
Indefinite iterated integrals. The integral
![]()
is an indefinite iterated integral. It is interpreted as
![]()
where the inner integral, ∫ f(x, y) dy, is integrated first, with respect to y, regarding x as a constant, and then the outer integration is performed with respect to x, regarding y as a constant. Each integration thus performed is called partial integration, and is the inverse of partial differentiation.
Example 1. Find
![]()
Solution.
![]()
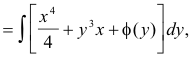
where the arbitrary function
![]() was introduced in order to provide the most general function
whose partial derivative with respect to x is x3 + y3. Now performing the remaining integration with
respect to y, we obtain
was introduced in order to provide the most general function
whose partial derivative with respect to x is x3 + y3. Now performing the remaining integration with
respect to y, we obtain
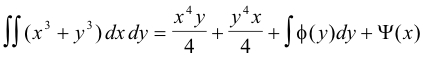
![]()
where Ψ(x) and Φ(y) are arbitrary functions.
One can confirm the same result will be obtained by reversing the order of integration.
The above integration is verified by observing that
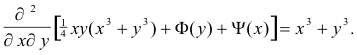
Definite iterated integrals. The integral
![]()
is a definite iterated integral where a and b are constants and u1 and u2 are either constants or functions of x. The inner integral is integrated first with respect to y, regarding x as constant, and then the outer integral is integrated with respect to x, regarding y as constant.
This notation can be extended to functions of any number of variables. Thus
![]()
represents a definite iterated integral in three variables.
Example 1. Evaluate
![]()
Solution.
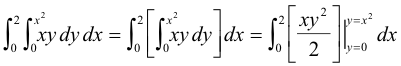
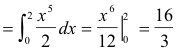
Area computation using double integrals.
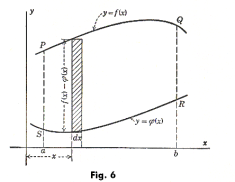
Problem. Compute the area of PQRS bounded by the curves y = f(x) and y = φ(x) and the ordinates at x = a and x = b shown in Fig. 6 using double integrals.
Solution.
![]()
If we were to compute this area using single integrals we would get
![]()
![]()
Note that this integral is exactly the same as
![]()
Example. Compute the area enclosed by the parabola y2 = 2x + 4 and the line y = x - 2. See Fig. 7.
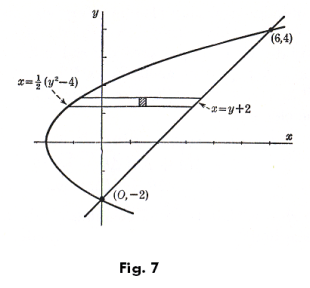
Solution. We will integrate first with respect to x, summing the little area elements in a horizontal strip extending from the parabola to the line. The limits of integration are from x = ½ (y2 - 4) to x = y + 2. We then sum these strips by integrating with respect to y between the limits y = -2 and y = 4. Thus
![]()
![]()
![]()
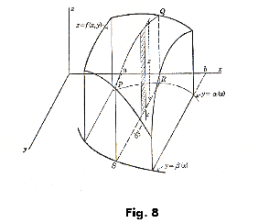
Volume computation by double integration.
Problem. Compute the volume between the xy-plane and the surface z = f(x, y), bounded on the sides by two arbitrary cylindrical surfaces y = α(x) and y = β(x), and the planes x = a and x = b, as shown in Fig. 8 using double integrals
Solution. The formula is
![]()
Example.
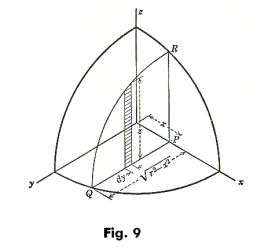
Express the volume of one octant of the sphere x2 + y2 + z2 = r2 as a double integral.
See Fig. 9.
Solution.
![]()
![]()
![]()
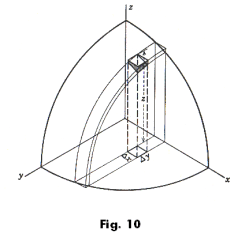
It is important to interpret this integration as a double summation process. The quantity z Δx Δy is
the volume of a rectangular column with base Δy by Δx and height z, as indicated in Fig. 10. One
can see that the first integration (with respect to y) sums these columns into a slice extending from y
= 0 to y =
![]() The second integration, then, sums all the slices from x = 0 to x = r.
The second integration, then, sums all the slices from x = 0 to x = r.
****************************
Triple integrals.
****************************
Def. Triple integral. Let f(x, y, z) be a function defined and continuous over a finite region R of xyz-space. Suppose that R is divided into n subregions R1, R2, ... ,Rn of volumes ΔV1, ΔV2, .... , ΔVn , respectively. In each subregion Rk we select a point Pk(xk, yk, zk) and form the sum
![]()
Next we define the diameter ri of a subregion Ri to be the greatest distance between any two points within or on its boundary. The triple integral of the function f(x, y) over the region R is then defined as
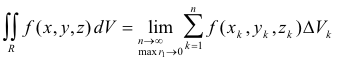
where we stipulate that the maximum ri → 0 as n → 0.
Evaluation of the triple integral.
Rectangular coordinates.
![]()
![]()
where the limits of integration are chosen to cover the region R.
Cylindrical coordinates.
![]()
where the limits of integration are chosen to cover the region R.
Spherical coordinates.
![]()
where the limits of integration are chosen to cover the region R.
Centroids and moments of inertia.
Centroids. The coordinates (
![]() ) of the centroid of a volume satisfy the relations
) of the centroid of a volume satisfy the relations
![]()
![]()
![]()
Moments of inertia. The moments of inertia of a volume with respect to the coordinate axes are given by
![]()
![]()
![]()
References.
Middlemiss. Differential and Integral Calculus.
Ayres. Calculus. (Schaum)
Sherwood, Taylor. Calculus.
Smith, Salkover, Justice. Calculus.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life