Approximate integration, Trapezoidal rule, Prismoidal formula, Simpson�s rule

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

APPROXIMATE INTEGRATION, TRAPEZOIDAL RULE, PRISMOIDAL FORMULA, SIMPSON’S RULE

Introduction. An approximate value of the integral

can be obtained by certain numerical formulas and by the use of mechanical integrators made for the purpose such as the polar planimeter. There are several reasons why one might choose to use one of these methods. Typically in practical work in science and engineering one is working with measured data that only has a certain accuracy. We are thus working with data that is approximate already. And the accuracy of the results can’t be expected, of course, to exceed that of the initial data. An approximating method may give an answer that is as accurate as we need. An approximating method may be the most practical. And in some cases we may be just unable to use regular integration. For example, often the integrand f(x) is defined by a table of values. Or the integral may not be expressible in terms of elementary functions. Or it might possibly be expressible in terms of elementary functions but just extremely difficult to integrate.

Often one of the various methods of approximate integration may indeed be just as good for our particular problem as regular integration and may be much easier and faster.

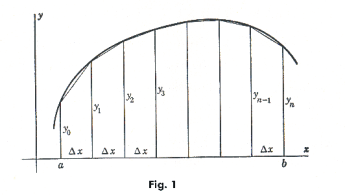
The trapezoidal rule. The trapezoid rule for approximating the value of the definite integral

is as follows:

Divide the interval from x = a to x = b into n equal subintervals of length Δx = (b - a)/n, erect ordinates y₀, y₁, y₂, ... , y_n as shown in Fig. 1, and join the tops of the ordinates by straight line segments. Then the sum of the areas of the trapezoids thus formed will be an approximation to the area under the curve. If we denote their sum by A_T, then

A_T = ½ (y₀ + y₁)Δx + ½ (y₁ + y₂)Δx + ...... + ½ (y_{n -1} + y_n)Δx

1) A_T = Δx[½ y₀ + y₁ + y₂ + ......... + y_{n -1}+ ½ y_n].

The accuracy of the approximation will depend upon the number of intervals used and upon the character of the function f(x). If f(x) is given as a table it must be remembered that formula 1) may be applied if and only if the spacings between abscissa points are equal. If the spacings are unequal one must use the following formula:

2) A_T = ½ (y₀ + y₁)Δx₁ + ½ (y₁ + y₂)Δx₂ + ...... + ½ (y_{n -1} + y_n)Δx_n

where Δx_i = x_i - x_{i -1}.

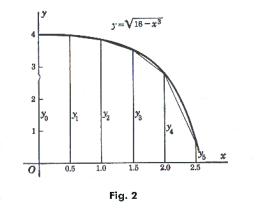
Example. Evaluate approximately

taking n = 5.

Solution. We divide the interval from x = 0 to x = 2.5 into 5 equal parts where the length of each part is Δx = 0.5. The following table gives the computed ordinates.

The trapezoidal formula then gives:

A = 0.5[ ½ (4) + 3.98 + 3.87 + 3.55 + 2.83 + ½ (0.61)] = 8.27.

See Fig. 2.

The prismoidal formula. The prismoidal formula for approximating the value of a definite integral is given in following theorem:

Theorem 1. If f(x) is a polynomial of degree 3 or less, then

In this equation f(a), of course, represents the value of the integrand when x = a, f(b) is its value when x = b, and is its value when the value of x is half-way between a and b.

Proof of Theorem

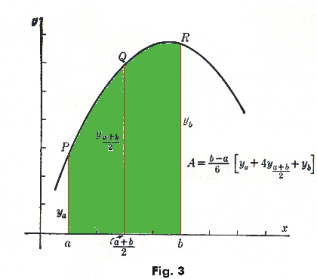
The geometrical interpretation is given by Fig. 3. Assuming that f(x) is a polynomial of degree 3 or less, then the area under the curve y = f(x) in the interval from x = a to x = b is given exactly by the formula

If f(x) is not a polynomial in x or if it is not of degree 3 or less, then 4) gives an approximation to the area by giving exactly the area under the parabola

y = Ax² + Bx + C

that passes through the points P, Q and R (Fig. 3). It may be remarked that the area under any cubic curve through P, Q, and R, in the interval from x = a to x = b, is equal to that under the parabola.

Example. Evaluate

using the prismoidal formula.

Solution. The values of the function 3x - ⅓x² when x = 1, 3, and 5 are respectively 8/3, 6, and 20/3. Consequently,

History of prismoidal formula. The prismoidal formula originated as an expression for the volume of any solid (such as prismoids and prismatoids) which may be suitably decomposed into prisms and related solids such as pyramids and frustums of pyramids. The prismoidal formula for the volume of any of these solids is

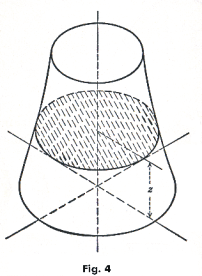
where A₁ and A₃ are the areas of the bases whose distance apart is h, and A₂ is the area of the cross-section of the solid in a plane parallel to the end planes and halfway between them.

This prismoidal formula 5) is a direct consequence of Theorem 1. Let the area of the cross section of the solid shown in Fig. 4, at a distance z above its base, be A(z). Then if the height of the solid is h, its volume is given by

If A(z) is a polynomial in z of degree 3 or less, then the value of this integral is, by Theorem 1,

where A₁, A₂, and A₃ denote the areas at the bottom, mid-section, and top, respectively.

The prismoidal formula 5) does in fact give the exact volume of a prismatoid, prismoid, prism, pyramid, frustum of a pyramid, wedge, cylinder, cone, frustum of a cone, sphere, ellipsoid, spherical segment, or, in general, any solid bounded by a quadric surface and two parallel planes. For in all these cases it may be shown that the area of the cross-section in any intermediate plane parallel to the end planes is a quadratic function of x.

For solids not satisfying the specified conditions, the prismoidal formula gives an approximation to the volume. The formula can be used with a fair degree of accuracy for almost any solid whose surface does not have sudden and extensive breaks and irregularities. If the surface is irregular it may be possible to divide the solid up into portions which approximate figures for which the formula holds. The formula is extensively used in earthwork and masonry computations. Engineers use it, for example, in estimating the volumes of such irregular solids as are encountered in making cuts and fills in road building.

Simpson’s Rule. 1. Divide the interval from x = a to x = b into n equal subintervals of length Δx = (b - a)/n where n must be an even number. 2. Erect ordinates y₀, y₁, y₂, ... , y_n as shown in Fig. 5. Simpson’s Rule states

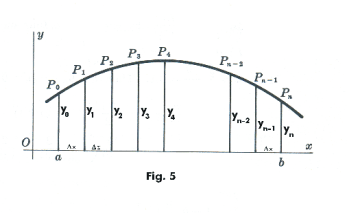
where the number of intervals must be even.

Simpson’s Rule is obtained by using the prismoidal formula to approximate the area under each of the arcs P₀P₁P₂, P₂P₃P₄, ...., P_n-2P_n-1P_n and then adding together the results. Thus

From previous considerations it is clear that this formula will give the value of the integral exactly if f(x) is a polynomial in x of degree not higher than 3.

References.

Middlemiss. Differential and Integral Calculus.

Smith, Salkover, Justice. Calculus

Oakley. The Calculus.