Integration, indefinite integral, fundamental formulas and rules

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

INTEGRATION, INDEFINITE INTEGRAL, FUNDAMENTAL FORMULAS AND RULES

Def. Indefinite integral. The indefinite integral of a function f(x) is a function F(x) whose derivative is f(x). The indefinite integral of a function is the primitive of the function. The terms indefinite integral, integral, primitive, and anti-derivative all mean the same thing. They are used interchangeably. Of the four terms, the term most commonly used is integral, short for indefinite integral. If F(x) is an integral of f(x) then F(x) + C is also an integral of f(x), where C is any constant.

Def. Integrate (a function). To integrate a function is to go through the process of finding the integral or primitive of the function.

Notation used to denote integrals. The notation used to denote the integral (or primitive) of a function f(x) is

This notation may seem a bit illogical, cumbersome and confusing to a first-time reader and he may wonder why such a complicated notation would be used to denote the primitive F(x) of a function f(x). Surely a simple notation such as Λ f(x) could be used to denote a primitive of f(x). Why use such a abstruse, confusing, cumbersome notation? Well, there are reasons behind the notation.

It is a notation that follows logically if we assume we can use the usual algebraic rules in the manipulation of differentials in equation form. The notation follows as a logical consequence of the rules. For example, consider the following.

By the definition of an integral or primitive we have the following relationship between a function f(x) and its primitive F(x):

Then, using algebraic rules of manipulation,

Taking the integral of both sides,

Thus, using rules of algebraic manipulation, we have started with

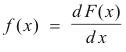
and deduced that the primitive F(x) is given by

Thus this notation allows us to use algebraic manipulation in solving integration problems.

In addition, most integration problems come in the form of definite integrals of the form

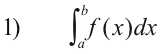
and we work algebraically from that form. The source of the notation is undoubtedly the definite integral. It is the definite integral without the limits. Indeed, if you view the upper limit b of the definite integral 1) as variable, replace it with x, then it becomes the area function

and the area function A(x) does indeed represent a primitive of f(x).

Fundamental integration formulas. The following are the main formulas and rules for integration, the most important of which need to be memorized. Many follow immediately from the standard differentiation formulas. a and m are constants.

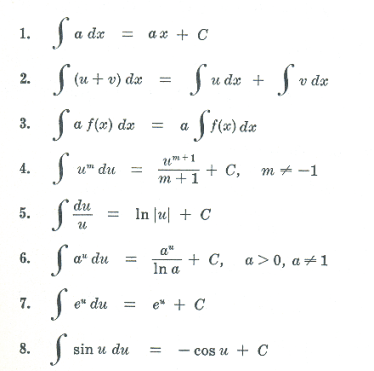
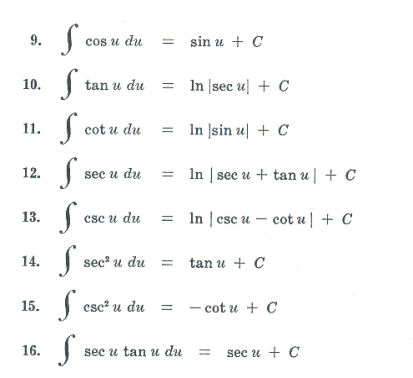
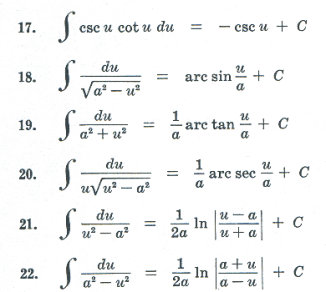
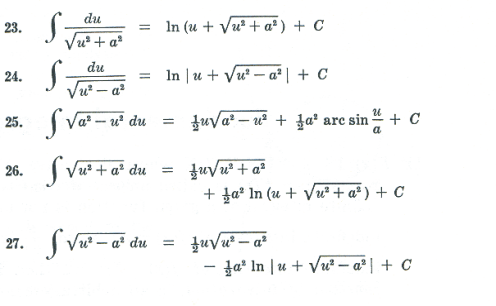
Def. Evaluate (an integral). To carry out the indicated integration, and if it is a definite integral, substitute the limits of integration.

The process of integration. The definition of the derivative carried with it a formal process by which one could find the derivative of a given function. Given any analytically defined function (algebraic, trigonometric, etc.) we can find the derivative of it through a fairly straightforward process. The situation with integration is different. There is no straightforward, direct process for integrating a function. The process goes like this: We are presented with an integral such as

to evaluate. To do it we ask ourselves, “What primitive has the differential f(x)dx?” We use our knowledge of memorized formulas and rules plus various techniques that we have learned plus perhaps integration tables to try to find a primitive, if one exists. There is no set procedure. Creativity and ingenuity are often needed. Typically we may do a lot of manipulating and experimenting. If we find a primitive F(x), then the integral is given as

where C is any constant.

If we are presented with a definite integral such as

to evaluate, then the solution will have the form

There is, however, no guarantee that a solution exists that is expressible in terms of elementary functions. For example, none of the functions

have primitives that can be expressed in terms of elementary functions. There is, for example, no finite combination of elementary functions (i.e. algebraic, trigonometric, exponential, etc.) whose derivative is .