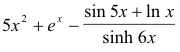
Website owner: James Miller
ELEMENTARY FUNCTIONS, GENERAL METHODS OF INTEGRATION
Elementary functions.
***************************
Consider the following set of functions which we shall call the Simple Elementary Functions. They are assumed to have complex arguments.
-----------------------------------------------------------------------------------------------------------------
The Simple Elementary Functions: c, x, xa, ex, ax, ln x, loga x, sin x, cos x, tan x, ..., sin-1 x, cos-1 x, tan-1 x, ... , sinh x, cosh x, tanh x, ..., sinh-1 x, cosh-1 x, tanh-1 x, ... where c and a are complex constants and x is a complex variable.
-----------------------------------------------------------------------------------------------------------------
The simple elementary functions include the familiar exponential, logarithmic, trigonometric and hyperbolic functions plus the variable x and the constant c. Utilizing the term “simple elementary function” we now define the term “elementary function”.
Def. Elementary function. An elementary function is any function that can be built from the simple elementary functions by the four arithmetic operations of addition, subtraction, multiplication and division and the operation of taking a function of a function, each of these operations being performed a finite number of times.
Example. Any complex expression built by these rules from the simple elementary functions is an elementary function. For example
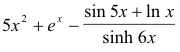
is an elementary function.
Note. All of the simple elementary functions themselves also qualify as being elementary functions, from the wording of this definition. However, the concept of an elementary function is that of a complex function built up of simple elementary functions. The simple elementary functions are often referred to as “the elementary functions”, a cause for some confusion.
The derivative of any elementary function is again an elementary function. However, the integral of an elementary function may not be an elementary function. The integral of an elementary function may lead to a function outside the set of elementary functions.
General methods of integration. Not every function can be integrated. Even if a function can be integrated the integral may not be an elementary function. Often one finds himself in a position of attempting to integrate some function by one device or another with no certainty that the integral exists. There are, however, certain large and important classes of functions which can be systematically integrated by general methods.
The following three classes of integrals can be systematically integrated in terms of elementary functions by general methods:
![]()
where R(x) is any rational function of x.
![]()
where R(sin x, cos x) is any rational function of sin x and cos x.
![]()
where P(x) is any first or second degree polynomial in x and R(x,
![]() ) is any
rational function of x and
) is any
rational function of x and
![]() .
.
Integrals of the following class can be integrated in terms of elliptic integrals:
![]()
where P(x) is any third or fourth degree polynomial in x with no repeated roots and R(x,
![]() ) is any rational function of x and
) is any rational function of x and
![]() .
.
By a suitable change of variable, such an integral can be reduced to a sum of elementary integrals and integrals of the following types:
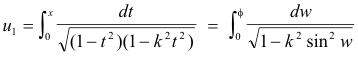
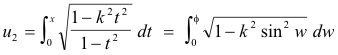
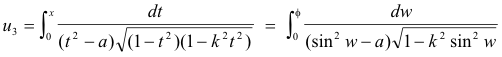
These are incomplete elliptic integrals of the first, second and third kind, respectively. When expressed in terms of t = sin w, they are Legendre’s normal forms. The constant k (0 < k < 1) is the modulus and a is an arbitrary constant. If f = π/2, the integrals are called complete.
Series evaluation of the elliptic integrals may be made and numerical tables for them are available. They are called elliptic because they were first studied in attempts to determine the circumference of the ellipse.
The International Dictionary of Applied Mathematics. Elliptic integral
***************************************
Integration of integrals of type
![]()
where R(x) is any rational function of x.
Procedure.
1] If the rational function R(x) is a complex expression, reduce it to a rational fraction i.e. to the form g(x) / G(x) where g(x) and G(x) are polynomials.
2] If the rational fraction g(x) / G(x) is improper reduce it to the sum of a polynomial and a proper fraction h(x) / H(x) ( a proper fraction has a numerator of lower degree than the denominator).
3] Reduce the proper fraction h(x) / H(x) to the sum of partial fractions of the type
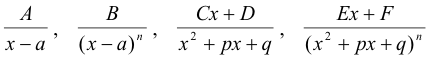
where n is a positive integer, p2 - 4q < 0, and the denominators of the fractions consist of the linear and irreducible quadratic factors of the polynomial H(x). Any proper fraction can be reduced to the sum of integrals of this type.
4] The evaluation of the integral
![]()
is now reduced to the evaluation of the integral of a polynomial plus integrals of the types
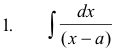
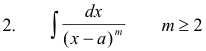
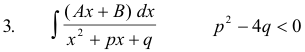
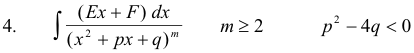
I Integration of integrals of types
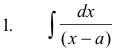
and
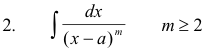
These integrals are immediately obtained using the formulas for the integrals of functions 1/u and un.
II Integration of integrals of type
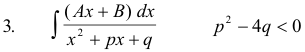
Case 1. p = 0. If p = 0, then q must be positive since p2 - 4q < 0. Set q = a2 and substitute into 3 giving
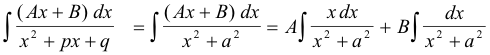
The integration is now immediate using formulas
![]()
![]()
Case 2. p
![]() 0. We can write
0. We can write
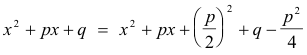
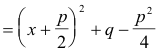
The quantity
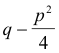
is positive, since p2 - 4q < 0.
Set
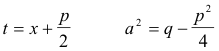
and we have
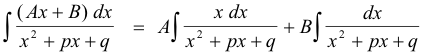
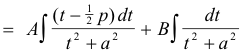
![]()
which can be immediately integrated using formulas (1) and (2) above.
III Integration of integrals of type
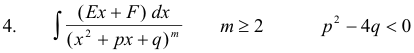
Again,
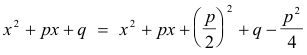
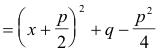
Set
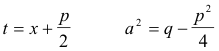
and we have
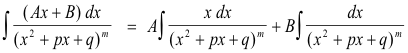
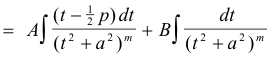
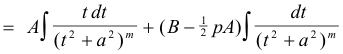
The integral
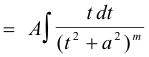
is immediately integrable using the power formula (i.e. substitute z = t2 + a2) and the integral
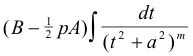
can be integrated using the reduction formula
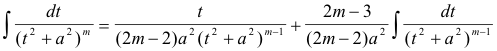
***************************************
Integration of integrals of type
![]()
where R(sin x, cos x) is any rational function of sin x and cos x.
Make the substitution
![]()
Then
![]()
From the following identity
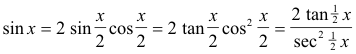
we deduce
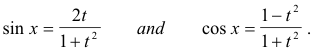
On substituting these values for sin x and cos x into R(sin x, cos x) we see that R(sin x, cos x) is a rational function of t i.e. R(sin x, cos x) = r(t). Thus we can integrate
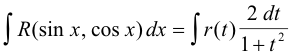
using the method for integrating rational functions.
***************************************
Integration of integrals of type
![]()
where
![]() is any rational function of x and y =
is any rational function of x and y =
![]() .
.
By “completing the square” we obtain
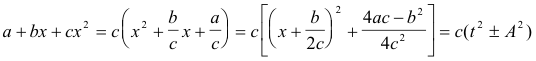
where
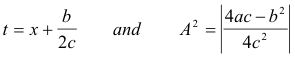
with the lower sign of c(t2
![]() A2) being used when 4ac - b2 is negative.
A2) being used when 4ac - b2 is negative.
Thus
![]()
There are three cases.
Case 1. 4ac- b2 < 0, c < 0. In this case the substitutions
![]()
will reduce the integral to the form
![]()
where R(sin x, cos x) is any rational function of sin x and cos x.
We then deal with it according to the procedure for that type.
Case 2. 4ac- b2 > 0, c > 0. In this case the substitutions
![]()
will reduce the integral to the form
![]()
where R(sin x, cos x) is any rational function of sin x and cos x.
We then deal with it according to the procedure for that type.
Case 3. 4ac- b2 < 0, c > 0. In this case the substitutions
![]()
will reduce the integral to the form
![]()
where R(sin x, cos x) is any rational function of sin x and cos x.
We then deal with it according to the procedure for that type.
References.
Osgood. Advanced Calculus. Chap. 1.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life