Website owner:  James Miller

SURFACE MAPS, CONFORMAL MAPS, ISOTHERMIC SURFACES, AREA-PRESERVING MAPS

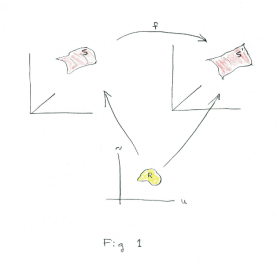
Surface maps. Two surfaces, S and S', are said to be mapped upon one another if there exists a one-to-one correspondence between the points of one surface and the points of the other. Let S be a simple surface element defined by the one-to-one mapping

            x = x(u, v)

1)        y = y(u, v)

            z = z(u, v)

of a region R of the uv-plane into xyz-space and let S' be a simple surface element defined by the one-to-one mapping

            x' = x'(u', v')

2)        y' = y'(u', v')

            z' = z'(u', v')

of a region Q of the u'v'-plane into x'y'z'-space. Then a mapping of a region of surface S onto a corresponding region of S' is given by the one-to-one mapping

3)        u' = u'(u, v)

            v' = v'(u, v)                              

of the region R into region Q. If we substitute equations 3) into equations 2), the variables x', y', z' of 2) become functions of the parameters u, v and corresponding points P and P' on surfaces S and S' have the same set of curvilinear coordinates u, v. Thus we can speak of the above equations as defining a mapping of surface S onto surface S' with the parameters u, v serving as curvilinear coordinates of corresponding points on the two surfaces. See Fig. 1.

Def. Conformal map or conformal transformation. A map that preserves angles. More explicitly, the map of S on S' is conformal if the angle between two directed curves through a point P of S is always equal to the angle between the two corresponding directed curves through the corresponding point P' of S'.

Theorem 1. Let surface S be mapped onto surface S'. Let C and C' be two corresponding curves passing through two corresponding points P and P' with differentials of arc ds and ds' at P and P'. A necessary and sufficient condition that the mapping of S onto S' be conformal is that the elements of arc ds and ds' be proportional.

Theorem 2. Let S be a simple surface element defined by the one-to-one mapping

            x = x(u, v)

            y = y(u, v)

            z = z(u, v)

of a region R of the uv-plane into xyz-space. This mapping from region R onto surface S is conformal if, and only if, the fundamental coefficients of the first order satisfy E = G = λ(u, v) 0, F = 0. The coordinates u, v are called conformal parameters.

Theorem 3. A mapping of a surface S onto a surface S' defined by

            x = x(u, v)

            y = y(u, v)

            z = z(u, v)

and

            x' = x'(u, v)

            y' = y'(u, v)

            z' = z'(u, v)

is conformal at regular points if, and only if, the linear elements ds and ds' at points P and P' of S and S' are proportional i.e.

            E'du² + 2F'dudv + G'dv² = ρ²(Edu² + 2Fdudv + Gdv²),

where ρ = ρ(u, v), or, what is the same thing, if E' : F' : G' = E : F : G .

A consequence of Theorem 1 is that in a conformal mapping of a surface S onto a surface S', a small figure (e.g. a triangle) at some point P on S is mapped into a figure that is almost similar to it at point P' on S', the more similar the smaller the figures are i.e. the figures are similar in the limit as ds 0. Thus a conformal map of a small region of a surface near a point on a plane is very nearly accurate in the angles as well as in the ratio of distances even though the map may give a very distorted picture of the region in the large.

The only conformal correspondences between open sets in three-dimensional Euclidean space are obtained by inversions in spheres, reflections in planes, translations, and magnifications.

Def. Isothermic map. A map of a (u, v)-domain D on a surface S in which the fundamental coefficients of the first order satisfy E = G = λ(u, v), F = 0. The map is conformal except at the singular points where λ = 0. The coordinates u, v are isothermic parameters.

                                                                                                James/James. Mathematics Dictionary.

Def. Isothermic system of curves on a surface. A system of two one-parameter families of curves on a surface such that there exist parameters u, v for which the curves of system are the parametric curves of the surface, and for which the first fundamental quadratic form reduces to λ(u, v)(du² + dv²).

                                                                                                James/James. Mathematics Dictionary.

Def. Isothermic surface. A surface whose lines of curvature form an isothermic system. All surfaces of revolution are isothermic surfaces.

                                                                                                James/James. Mathematics Dictionary.

Def. Isothermic family of curves on a surface. A one-parameter family of curves on the surface such that the family together with its orthogonal trajectories forms an isothermic system of curves on the surface.

                                                                                                James/James. Mathematics Dictionary.

Def. Area-preserving map. A map which preserves areas.

Syn. Equivalent map, equiareal map.

Theorem 4. Let S be a simple surface element defined by the one-to-one mapping

            x = x(u, v)

            y = y(u, v)

            z = z(u, v)

of a region R of the uv-plane into xyz-space. This mapping from region R onto surface S is area-preserving if, and only if, the fundamental coefficients of the first order satisfy EG - F² = 1.

Theorem 5. A mapping of a surface S onto a surface S' defined by

            x = x(u, v)

            y = y(u, v)

            z = z(u, v)

and

            x' = x'(u, v)

            y' = y'(u, v)

            z' = z'(u, v)

is area-preserving if, and only if, E'G' - F'² = EG - F².

References.

1. James/James. Mathematics Dictionary.

2. Graustein. Differential Geometry.

3. Struik. Lectures on Classical Differential Geometry.