Isometric mapping, intrinsic property

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

ISOMETRIC MAPPING, INTRINSIC PROPERTY

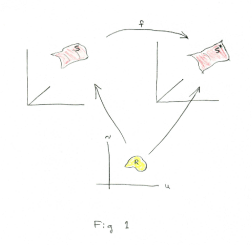
Isometric mapping (or isometry). An isometric mapping is a mapping that preserves lengths. A one-to-one mapping f of a surface S onto a surface S* is called an isometric mapping or isometry if the length of an arbitrary arc on S is equal to the length of its image on S*. See Fig. 1. If f is an isometry from S to S*, then f ^-1 is an isometry from S* to S.

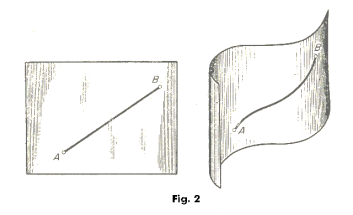
If an isometry exists from S to S*, then the surfaces S and S* are said to be isometric. Bending type deformations, where there is no stretching or shrinking, as in the bending of a flexible sheet, provide examples of isometries. One can see that if a sheet of paper is bent smoothly into various shapes, lengths are preserved and the intrinsic geometry of the sheet is preserved.. See Fig. 2.

Theorem 1. Let S be a simple surface element defined by the one-to-one mapping

x = x(u, v)

1) y = y(u, v)

z = z(u, v)

of a region R of the uv-plane into xyz-space. In this mapping from region R onto surface S lengths are preserved if, and only if, the fundamental coefficients of the first order satisfy E = G = 1, F = 0. In this case, the coordinates u, v are called isometric parameters.

Theorem 2. Let a one-to-one mapping f of a surface S onto a surface S* be given by

x = x(u, v)

1) y = y(u, v)

z = z(u, v)

and

x* = x*(u, v)

2) y* = y*(u, v)

z* = z*(u, v)

where the first fundamental coefficients of 1) are E, F, G and the first fundamental coefficients of 2) are E*, F*, G*. Then the mapping f is isometric if and only if E = E*, F = F*, G = G*.

Theorem 3. A necessary and sufficient condition for a mapping to be isometric is that it be conformal and area-preserving.

Intrinsic property. The term “intrinsic property” carries the connotation of an invariant, inherent or unchanging property. One needs to ask the question, “Invariant in regard to what?” A property may be invariant with respect to one kind of transformation such as a change of coordinate system, a projective transformation, or an isometric transformation and changing with respect to another. The term “intrinsic property” has in fact been assigned one specific meaning in regard to curves and another meaning in regard to surfaces, a possible cause for confusion. When used in reference to curves it means a property that is invariant in regard to a change of coordinate system. When used in reference to surfaces it means a property that is invariant in regard to isometric transformations. The following two definitions from the James & James Mathematics Dictionary indicates this shift in meaning in going from curves to surfaces.

Intrinsic properties of a curve. Properties that are not altered by any change of coordinate systems. Some of the intrinsic properties of conics are their eccentricity, distances from foci to directrices, length of latus rectum, length of axes (or an ellipse or hyperbola), and their reflective properties.

Intrinsic property of a surface. A property which pertains merely to the surface, not to the surrounding space; a property which is preserved under isometric transformations; a property expressible in terms of the coefficients of the first fundamental quadratic form only.

Thus an intrinsic property of a surface is a property that remains invariant under an isometric mapping. It follows from Theorem 2 that a property of a surface is an intrinsic property if and only if it depends only on the first fundamental form.

Let us now consider a particular property of a surface: the normal curvature k_n of a surface S at some point P. This property will be invariant in regard to a change of coordinate system but will not be invariant under the kind of bending deformation illustrated by Fig. 2 above. This is reflected in the fact that k_n is dependent on both the first and the second fundamental coefficients. Only properties that depend only on the first fundamental coefficients E, F and G are invariant under such a bending deformation.

Intrinsic geometry of a surface. All the properties of a surface that are not changed by deformations that preserve length (i.e. bending deformations) make up what is called the intrinsic geometry of the surface.

Let us now make a list of those properties that are preserved and those properties that are not preserved under an isometric mapping of a surface S.

A. Properties preserved by an isometric mapping. distance, angle, area, total curvature, geodesic curvature, geodesics.

B. Properties not preserved by an isometric mapping. mean curvature, normal curvature, geodesic torsion, curvature and torsion of a curve on the surface, lines of curvature, asymptotic lines.

Properties A all depend on the first fundamental coefficients E, F, G only and properties B depend on both E, F, G and L, M, N.

Let us now make the following observation: properties A all pertain to the surface itself and are independent of the relationship of the surface to the space in which it is embedded. For example, if we bend a sheet of paper with some figures on it, as in Fig. 2 above, distances, angles, areas, etc. on the paper remain unchanged irregardless of how the paper is embedded in surrounding space. On the other hand, properties B, properties such as normal curvature, the curvature and torsion of a curve on the surface, etc. change under the bending of the paper. They are dependent on how the surface (the paper) is embedded in space.

● Isometric mappings are associated with one specific type of geometric operation, namely the bending of a surface without stretching, compressing or tearing it. Any deformation of any other type stretches, compresses or tears it. And only certain kinds of surfaces can be bent.

Def. Applicable surfaces. Two surfaces are said to be applicable to one another if one can be deformed into the other by bending, with no stretching, compressing or tearing.

References.

1. Mathematics, Its Contents, Methods and Meaning. Vol. II, Chapter VII.

2. Lipschutz. Differential Geometry. Chapter 11.

3. James/James. Mathematics Dictionary.

4. Graustein. Differential Geometry.