Christoffel symbols of the first and second kind

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

CHRISTOFFEL SYMBOLS OF THE FIRST AND SECOND KIND

Christoffel symbols. Christoffel symbols are shorthand notations for various functions associated with quadratic differential forms. The differential form is usually the first fundamental quadratic form of a surface. Each Christoffel symbol is essentially a triplet of three indices, i, j and k, where each index can assume values from 1 to 2 for the case of two variables, or from 1 to n in the case of a quadratic form in n variables. Associated with different combinations of values of the three indices are different functions.

Christoffel symbols of the first kind. For the quadratic differential form in two variables

the Christoffel symbols of the first kind are defined as

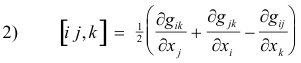
where the indices i, j and k can each assume the values of either 1 or 2.

Examples

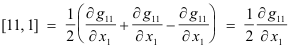
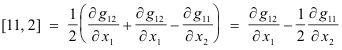
Other notations. Other notations, instead of [i j, k], are used. They include C_ij^k and Γ_ijk and

Meaning for the First Fundamental Quadratic Form. Let us examine the meaning of these Christoffel symbols for the first fundamental quadratic form

3) Edu² + 2Fdudv + Gdv² .

Let S be a simple surface element defined by the one-to-one mapping

x = x(u, v)

y = y(u, v)

z = z(u, v)

of a region R of the uv-plane into xyz-space. Let

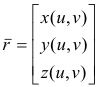
be the position vector to point P on the surface. Let us use subscript notation to denote partial differentiation i.e.

The first fundamental quadratic form is

where:

The functions that correspond to the different possible combinations of values of the indices i, j and k of the Christoffel symbol are [as can be confirmed by plugging the index values into 1)]:

The equivalence of the E, F and G expressions in terms of the is easily confirmed by taking the indicated partial derivatives of

The source of the Christoffel symbol notation becomes clear with a slight change in notation. If we use an integer subscript notation for the partial derivatives where

then

The Christoffel symbols are symmetric in i and j, which means that

[i j, k] = [j i, k] .

Also, by definition, g_ij = g_ji.

Christoffel symbols of the second kind. For the quadratic differential form in two variables

the Christoffel symbols of the second kind are defined as

Γ_i _j^k = A_k1[i j, 1] + A_k2[i j, 2]

where

1] the indices i, j and k can each assume the values of either 1 or 2,

2] A_ki = C_ki/Δ

where C_ki is the cofactor of g_ki in the determinant

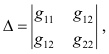
3] [i j, k] are the Christoffel symbols of the first kind.

For the first fundamental quadratic form

3) Edu² + 2Fdudv + Gdv² .

the functions that correspond to the different possible combinations of values of the indices i, j and k are

Also,

The symbols in this case are also given by the following formulas:

The Christoffel symbols of the second kind correspond to the coefficients in the following equations of Gauss, from which they have their origin:

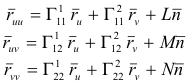
is the unit normal to the surface at point P and L,M, N are the second fundamental coefficients.

Quadratic form in n variables. For a quadratic form in n variables

as might be encountered in differential geometry investigations in n-dimensional space, we remark that Christoffel symbols are also defined. Here the indices i, j and k can each assume values 1, 2, ... , n. It is assumed that g_ij = g_ji for all i and j. The general definition for n variables reduces to formula 2) above for the case of two variables.

References.

1. Graustein. Differential Geometry.

2. Lipschutz. Differential Geometry. Chapter 9.

3. James/James. Mathematics Dictionary.

4. Eisenhart. A Treatise on the Differential Geometry of Curves and Surfaces.

More from SolitaryRoad.com:

The Way of Truth and Life

God's message to the world

Jesus Christ and His Teachings

Words of Wisdom

Way of enlightenment, wisdom, and understanding

Way of true Christianity