Dupin indicatrix, asymptotic directions and lines

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

DUPIN INDICATRIX, ASYMPTOTIC DIRECTIONS AND LINES

Dupin indicatrix of a surface at a point. Let P be some point on a surface S. Consider an xy-coordinate system where the x-axis represents the direction of minimum curvature k₁ and the y-axis represents the direction of maximum curvature k₂ at point P. The Dupin indicatrix of the surface at point P depends on the value of the total (Gaussian) curvature K = k₁k₂ at point P as follows:

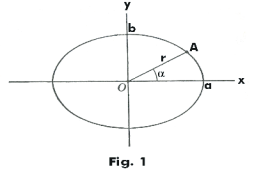
K > 0. The Dupin indicatrix is the ellipse

|k₁| x² + |k₂| y² = 1

See Fig. 1.

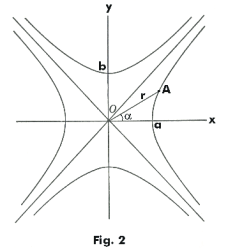
K < 0. The Dupin indicatrix is a set of conjugate hyperbolas

k₁ x² + k₂ y² = 1

k₁ x² + k₂ y² = -1

See Fig. 2.

K = 0. The Dupin indicatrix is a set of parallel lines corresponding to one of the forms

x² = |1/k₁| or y² = |1/k₂|

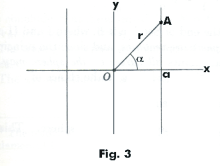
See Fig. 3.

We will now examine these three cases in detail.

Case 1. K > 0. k₁ and k₂ have the same sign, the surface at point P is bowl shaped, and point P is an elliptic point. Let us suppose that k₁ and k₂ are both positive. Then the Dupin indicatrix at point P is the ellipse

1) k₁x² + k₂y² = 1

shown in Fig. 1. Let us compute the distance r from the origin to point A. The equation of line OA is

2) y = x tan α .

We find the coordinates (x, y) of point A by solving equations 1) and 2) simultaneously. If we substitute 2) into 1) we obtain

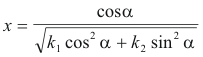
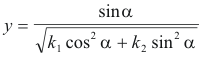
The distance r is then given by

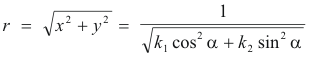
and since

k₁(α) = k₁ cos² α + k₂ sin² α ,

where k_n(α) is the normal curvature at point P in the direction α , we have

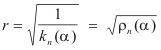
where ρ_n(α) is the radius of normal curvature in the direction α. The x and y intercepts Oa and Ob are

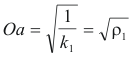
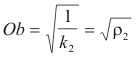
where ρ₁ and ρ₂ are the radii of normal curvature corresponding to k₁ and k₂.

Case 2. K < 0. k₁ and k₂ have opposite signs, the surface at point P is saddle shaped, and point P is a hyperbolic point. The Dupin indicatrix is a set of conjugate hyperbolas

k₁ x² + k₂ y² = 1

k₁ x² + k₂ y² = -1

shown in Fig. 2. As in Case 1, and by the same type analysis, the values of r, Oa and Ob are

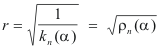
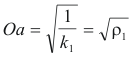
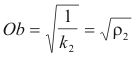
The two asymptotes of the hyperbolas are lines representing directions at which k_n(α) = 0. As the angle α increases and passes over an asymptote a passage occurs from one hyperbola to the other along with a change in sign of k_n(α).

Case 3. K = 0. Either k₁ = 0 or k₂ = 0, the surface at point P is a parabolic cylinder, and point P is a parabolic point. If k₁ = 0 the Dupin indicatrix is a set of parallel lines corresponding to the equation

y² = |1/k₂| .

If k₂ = 0 the Dupin indicatrix is a set of parallel lines corresponding to the equation

x² = |1/k₁| .

As in the other cases, and by the same type analysis, the values of r, and Oa are

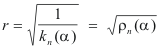
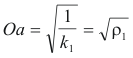
Overview. The above three cases represent the different locii to which the equation

k₁ x² + k₂ y² = 1

can give rise depending on the various possible combinations of signs and values of the constants k₁ and k₂. The Dupin indicatrix of a surface S at a point P is a device for gaining insight into the character of the surface near P. The curve of intersection of S and a nearby plane parallel to the tangent plane at P is approximately similar to the Dupin indicatrix. In the case of a hyperbolic point the surface S lies on both sides of the tangent plane so we need to intersect the surface with two planes close to the tangent plane, parallel to it, one on each side. If S lies entirely on one side of the tangent plane intersection by a single plane is adequate.

Asymptotic directions. A direction at a point P on a surface for which

1) L du² + 2M du dv + N dv² = 0

is called an asymptotic direction. Because the denominator of

is positive definite, the asymptotic directions are also the directions in which k_n = 0. At an elliptic point there are no asymptotic directions, at a hyperbolic point there are two distinct asymptotic directions, at a parabolic point there is one asymptotic direction and at a planar point every direction is asymptotic.

Asymptotic lines. A curve on a surface which is tangent to an asymptotic direction at every point is called an asymptotic line. Thus a curve on a surface element is an asymptotic line if and only if at each point of the curve the direction of the tangent to the curve satisfies 1). At a hyperbolic point equation 1) has two real distinct factors of the form Adu + Bdv = 0 which can be regarded as first order differential equations of the asymptotic lines.

Theorem 1. The u and v coordinate curves on a surface element are asymptotic lines if and only if at each point L = N = 0.

References.

1. Graustein. Differential Geometry.

2. Lipschutz. Differential Geometry

3. James/James. Mathematics Dictionary.

4. Struik. Lectures on Classical Differential Geometry.