Website owner: James Miller
CURVES IN THE PLANE, DERIVATIVE OF ARC LENGTH, CURVATURE, RADIUS OF CURVATURE, CIRCLE OF CURVATURE, EVOLUTE
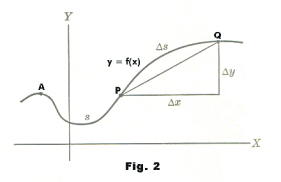
Derivative of arc length. Consider a curve in the x-y plane which, at least over some section of interest, can be represented by a function y = f(x) having a continuous first derivative. Let A be some fixed point on the curve and denote by s the arc length from A to any other arbitrary point P(x, y) on the curve. Let Q be a point at coordinates (x + Δx, y + Δy). See Fig. 2. Denote by Δs the arc length from P to Q. Then the instantaneous rate of change of arc length s per unit change in x is given by

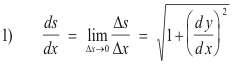
If a curve is given by the parametric equations
x = f(u)
y = g(u)
the rate of change of arc length s with respect to u is given by
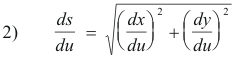
Note that both equations 1) and 2) can be derived from the following fundamental relationship:
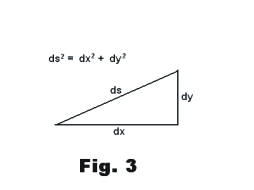
3) ds2 = dx2 + dy2
See Fig. 3. The relationships 1), 2) and 3) are important, much used forms. The relationship
ds2 = dx2 + dy2
reveals that ds is the hypotenuse of a right triangle with edges dx, and dy, a fact which is intuitively obvious since the arc Δs approaches the chord PQ as the chord approaches zero.
If we are dealing with arcs in three dimensional space instead of the plane, 3) becomes
4) ds2 = dx2 + dy2 + dz2
where ds is the diagonal of a rectangular parallelepiped (or box) with edges dx, dy and dz.
Curvature. Intuitively the curvature of a plane curve at a point P can be thought of as the curvature of that circle which approximates the curve most closely near that point. The curvature of a circle is directly defined by the length of its radius. The shorter the radius, the greater the curvature of the arc in the vicinity of any point P on it. The longer the radius, the bigger the circle, and the less the curvature of the arc in the vicinity of any point P on it. For a very large circle the curvature of an arc at some point P approaches that of a straight line i.e. zero curvature. In the following we will give the technical definition of curvature. We will find that this definition leads directly to the result that the curvature, K, of a circle is equal to the reciprocal of its radius r i.e. K = 1/r. Thus, for a circle, the length of its radius is a direct measure of its curvature.
Technical definition of curvature. Consider any smooth curve. Curvature measures the rate at which the tangent line turns per unit distance moved along the curve. Or, more simply, it measures the rate of change of direction of the curve.
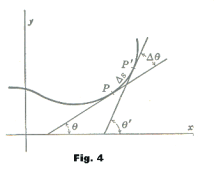
Let P and P' be two points on a curve, separated by an arc of length Δs. See Fig. 4. Then the average curvature of the arc from P to P' is expressed by the fraction
![]()
where Δθ = θ'- θ is the angle turned through by the tangent line moving from P to P'. The curvature K at point P is defined as
![]()
To find dθ/ds we use the formula
![]()
To compute dθ/dx first observe that tan θ = dy/dx so θ = arctan(dy/dx). Consequently,
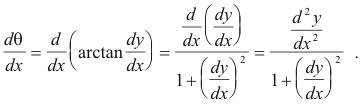
The quantity dx/ds is given by
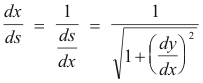
so the formula for curvature is
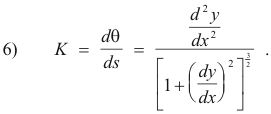
The sign of K will be positive if d2y/dx2 is positive and negative if it is negative. Many authors, however, regard the curvature as the absolute value of K, thus considering curvature as always positive.
Alternate formula for curvature. An alternate formula for curvature is
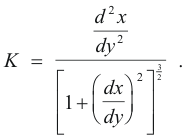
This formula can be used at a point where dy/dx doesn’t exist such as a point on a curve where the tangent line is parallel to the y-axis.
Example. Find the curvature of the cubical parabola y = x3 at (1, 1).
Solution.
dy/dx = 3x2
d2y/dx2 = 6x
dy/dx]1,1 = 3
d2y/dx2]1,1 = 6
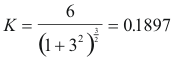
Curvature of a circle. Given a circle of radius R as shown in Fig. 5. The tangent line to the circle at P makes an angle θ with the x-axis. In moving to the position P' it turns through an angle Δθ. The amount of turning per unit distance moved along the arc is
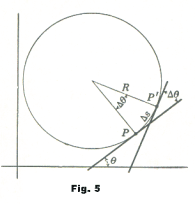
![]()
since Δs = RΔθ, θ being measured in radians.
Thus
![]()
The curvature of a circle is constant and is equal to the reciprocal of the radius.
Example. The curvature of a circle whose radius is 5 ft. is
![]()
This means that the tangent line, in traversing the circle, turns at a rate of 1/5 radian per foot moved along the arc.
Def. Radius of curvature. The radius of curvature for a point P on a curve is defined as
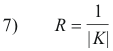
where K is the curvature.
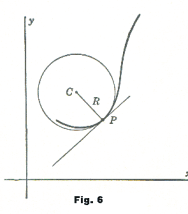
Def. Circle of curvature. Let R be the radius of curvature at a point P on a curve. The circle of curvature or Osculating Circle of the curve at point P is the circle of radius R lying on the concave side of the curve and tangent to it at P. See Fig. 6.
To construct the circle of curvature: On the concave side of the curve construct the normal at P and on it lay off PC = R. The point C is the center of the required circle.
The circle of curvature of a curve at a point P is that particular circle which has the same curvature as the curve itself at point P. Of the indefinitely large number of circles that can be drawn tangent to the curve at P, this is the only one whose curvature is the same as that of the curve at the point of contact. It can be shown that this circle “fits” the curve more closely in the neighborhood of P than any other circle — just as the tangent line fits it more closely than any other line.
Another definition of the circle of curvature at point P is as follows: Suppose we pass a circle through P and two arbitrarily selected neighboring points P' and P'' on the curve. The limiting position of this circle as P' and P'' both approach P along the curve can be shown to be identical with that of the circle of curvature as defined above.
Center of curvature. The center of curvature for a point P(x, y) of a curve is the center C of the circle of curvature at P. The coordinates (α, β) of the center of curvature are given by
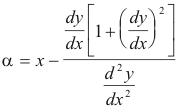
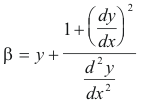
or
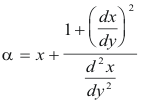
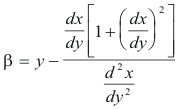
Def. Evolute. The evolute of a curve is the locus of the centers of curvature of a given curve.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life