Computation of the principal curvatures k₁ and k₂

The problem of computing the values of k₁ and k₂ is that of finding the maxima and minima of the function

where du and dv are viewed as variables (rather than differentials). For clarity let us replace du by x and dv by y. Our problem then is to find the maxima and minima of the function

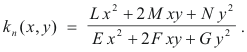
Let us also introduce the notation

            p(x, y) = Lx² + 2Mxy + Ny²

            q(x, y) = Ex² + 2Fxy + Gy²

Thus

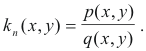
The requirement for k_n(x, y) to have a maxima or minima at a point (x, y) is that the following two conditions be met:

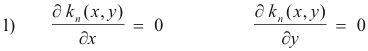
Using the formula from calculus

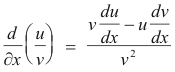
we compute the partial derivatives of

with respect to x and y as

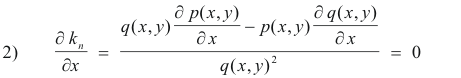
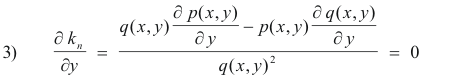
which can be written more concisely as

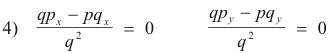
where

5)        p_x = 2L x + 2M y

            q_x = 2E x + 2F y

            p_y = 2M x + 2N y

            q_y = 2F x + 2G y .

If we multiply equations 4) by q we obtain

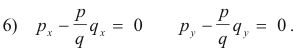
Now make the substitution

            k_n = p/q

and 6) becomes

7)        p_x - k_nq_x = 0             p_y - k_nq_y = 0

Now substituting the values of p_x, q_x, p_y, q_y from 5) into 7) we obtain

8)        (L - k_nE) x + (M - k_nF) y = 0

            (M - k_nF) x + (N - k_nG) y = 0

We wish to solve equations 8) for x and y. It is a homogeneous system and will have a nontrivial solution only if the determinant of the coefficients is equal to zero i.e. only if

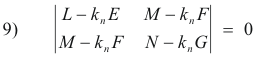
If we expand 9) we obtain the equation

10)      (EG - F²)k_n² - (EN + GL - 2FM)k_n + (LN - M²) = 0 .

Solving this equation for k_n will give us two values, k₁ and k₂, which will represent the minimum and maximum values of the function k_n(x, y) i.e. the principal curvatures.