Prove: Euler’s theorem. At each point P on a surface there exist two particular directions such that

1. They are mutually perpendicular.

2. The curvatures k₁ and k₂ of the normal sections in these directions are the smallest and the largest values of the curvatures of all normal sections at point P (in the particular case where k₁ = k₂ the curvature of all sections is the same, as for example, on a sphere).

3. Let φ be the angle, in the tangent plane, measured counterclockwise from the direction of minimum curvature k₁ . Then the normal curvature k_n(φ) in direction φ is given by

            k_n(φ) = k₁ cos²φ + k₂ sin²φ

Proof. For the proof of Euler’s theorem we need the following lemma.

Lemma. If the function f(x, y) has continuous second derivatives at a given point P, then there exists a rotation of the axes

            x = x' cos α - y' sin α

            y = x' sin α + y' cos α

that will reduce the mixed derivative f_xy at point P to zero.

Stated a little differently the lemma says that if the function z = f(x, y) has continuous second derivatives at a given point P then there exists some angle α by which the coordinate system can be rotated about the z axis that will make f_{x' y'} = 0.

Proof. Using the chain rule of partial differentiation

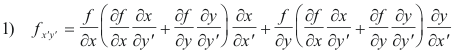
Now

so

or

From 3) it readily follows that for a value of α satisfying

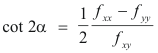
End of proof.

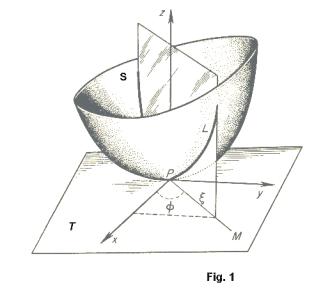
Proof of Euler’s theorem. Consider the surface S given by the equation z = f(x, y) in which the coordinate system has its origin at the point of interest P with its x and y axes lying in tangent plane T and so chosen as to make f_xy (0, 0) = 0. See Fig. 1. Now draw a line PM in the xy-plane making an angle with the x axis and consider the normal section L in the direction of this straight line. The curvature of L at point P, taking sign into account, is given by

where f(x, y) is the distance of a point on L to line PM.. Expanding f(x, y) by Taylor’s formula and noting that f_x(0, 0) = f_y(0, 0) = 0 (since the x and y axes lie in the tangent plane) we get

            f(x, y) = ½ (f_xx x² + f_yy y²) + ε

where ε is a higher order infinitesimal that approaches zero as x and y approach zero. For a particular point on L, x = ξ cos , y = ξ sin and thus

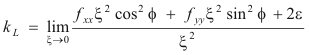
or

If we set , in 4) we find that f_xx and f_yy are the curvatures k₁ and k₂ of the normal sections in the directions of the x and y axes. Thus 4) is Euler’s formula

            k = k₁ cos² + k₂ sin² .

The fact that k₁ and k₂ are the minimal and maximal curvatures also follows from the formula. The maxima and minima of the function are found by finding the values of at which dk/d = 0. Differentiation shows that

and this function is equal to zero at = 0, π/2, π, ...