Prove: The normal curvature at point P is given by

where E, F, G, L, M, N are the fundamental coefficients of the first and second order.

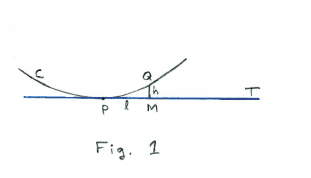
Proof. Let curve C shown in Fig. 1 be the normal section at point P in the direction of angle α. Shown in the figure is the tangent T at point P, Q a point on the curve near P, QM, a line perpendicular to the tangent, h = QM and l = PM . Then the curvature is given by

Now

and

so