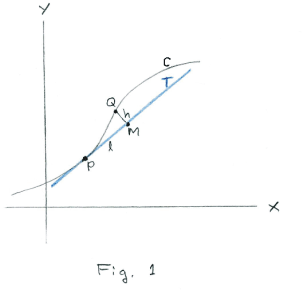
Prove. Given a plane curve C shown in Fig.1. Let T be the tangent to the curve at point P, Q be a point on the curve near P and let QM be a line perpendicular to the tangent. Let h = QM and l = PM as shown in the figure. Let k be the curvature of the curve at point P. Then we have the following relationship between k, l and h: 

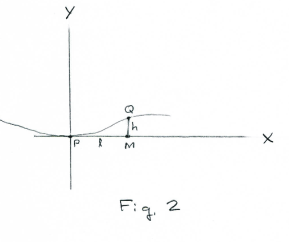
Proof. To prove this we choose a rectangular coordinate system in which point P lies at the origin and the x axis lies along the tangent as shown in Fig.2. We will view curve C as shown in Fig.2 as being represented by the function y = f(x). The general formula for the curvature at any selected point P on a curve y = f(x) is given by

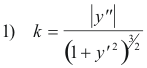
Here in our case y' = 0 and plugging this value into 1) gives k = |y''| . Let us now expand the function y = f(x) about the point x = 0 using Taylor’s Formula. We get  

            y = ½ y''x² + ε

where ε is an infinitesimal of higher order that can be neglected. Thus

and since |y| = h and x² = l² we have