Surfaces, surface representation, simple surface elements, curvilinear coordinates, surface normals, surface curves, first and second fundamental quadratic forms, osculating paraboloid, surface area

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

SURFACES, SURFACE REPRESENTATION, SIMPLE SURFACE ELEMENTS, CURVILINEAR COORDINATES, SURFACE NORMALS, SURFACE CURVES, FIRST AND SECOND FUNDAMENTAL QUADRATIC FORMS, OSCULATING PARABOLOID, SURFACE AREA

Three common methods for the analytical representation of a surface. Three methods are commonly used to represent surfaces. They are

1] Surface representation 1. An equation of form

z = f(x, y)

where f is a single-valued continuous function defined on a region R of the xy-plane.

2] Surface representation 2. An equation of the form

f(x, y, z) = 0

3] Surface representation 3. Parametric equations of the form

x = f(u, v)

1) y = g(u, v)

z = h(u, v)

where f, g, h are continuous functions defined on a connected region R of the uv-plane.

Equations 1) of Surface Representation 3] do not necessarily map in a one-to-one fashion. That is, more than one point (u, v) may map into the same point (x, y, z). Because of this fact the “surface” produced by the system may sometimes be something quite different from the usual conception of a surface. To avoid this, a stipulation that it is one-to-one needs to be appended. We do this in the concept of a simple surface element.

Simple surface element. Let R be a simply connected region (i.e. a bounded region such as a rectangular or circular region without “holes”) of the uv-plane. Let equations

x = x(u, v)

y = y(u, v)

z = z(u, v)

define a bicontinuous one-to-one mapping of R onto a point set S in xyz-space. Let

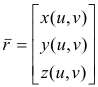
be the position vector to point P on the surface and let the condition

hold for all points in R. Then S is called a simple surface element.

For brevity we will refer to a simple surface element using the notation S: .

A simple surface element may be viewed as any configuration which may be obtained from a rectangular plane region by continuous deformation (bending, twisting, stretching, shrinking) without tearing and without bringing any points together which were originally distinct. A simple surface element can be described as a patch of surface in space enclosed by a boundary — where the boundary points are images of the boundary points of region R under the mapping. Thus this excludes surfaces of infinite extent such as an infinite cylinder and closed surfaces such as a sphere or a torus. It includes such surfaces as a plane circular region or a hemispherical surface.

Any surface, however, be it a torus, sphere, cylinder or whatever, may be viewed as consisting of a collection of simple surface elements. That is, any surface can be divided up into regions viewed as simple surface elements.

Def. Class of a surface. Let S be a simple surface element defined by the one-to-one mapping

x = x(u, v)

1) y = y(u, v)

z = z(u, v)

of a region R of the uv-plane into xyz-space. The surface element is said to be of class C ^m if the defining functions 1) have continuous derivatives of the m-th order.

Curvilinear coordinates of a point on a surface. Given two coordinate systems, a u-v coordinate system and an X-Y-Z coordinate system. See Figure 1. The parametric equations

x = x(u, v)

2) y = y(u, v)

z = z(u, v)

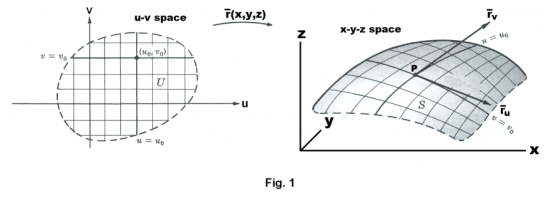
assign a point (x, y, z) in the X-Y-Z system to each number pair (u, v) in the u-v system. The number pair (u, v) can be considered a set of coordinates for a point P(x, y, z). The numbers (u, v) are called the curvilinear coordinates of point P. If we regard v as fixed in system 2) i.e. v = c, a constant, then system 2) becomes a system in a single variable u describing a space curve where u is the varying parameter. For each different value of v there is a separate space curve. These curves are called u-curves. Similarly one can let u = k, a constant, and obtain a v-curve where v is the varying parameter. One thus obtains families of u-curves and v-curves. The u-curves and v-curves are called coordinate curves. These coordinate curves form a curvilinear net on the surface similar to the coordinate net on a plane. The locus of all these coordinate curves form the simple surface element S. See Fig. 1. In the figure

Property of being smooth. A surface is called smooth at a point P if it has a tangent plane at each point in the neighborhood of P, and if the direction of the normal to this plane varies continuously from point to point.

Theorem 1. Let S: be a simple surface element. Then at any point P on S

where j₁, j₂, j₃ are the following Jacobians:

Proof.

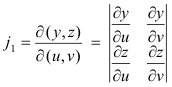
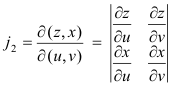
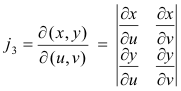
Corollary.

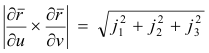
Directions of surface normals. If a surface is smooth at a point it will have a normal at that point.. The directions of the normals are as follows:

Surface representation 1. z = f(x, y). The direction of the normal at a point P is given by the set of direction numbers

evaluated at point P. The surface is smooth at P if f has continuous first partial derivatives there.

Surface representation 2. f(x, y, z) = 0. The direction of the normal at a point P is given by the set of direction numbers

evaluated at point P. The surface is smooth at P if f has continuous first partial derivatives there.

Surface representation 3. Parametric equations of the form

x = x(u, v)

y = y(u, v)

z = z(u, v)

The direction of the normal at a point P is given by the vector

where is the position vector of point P i.e.

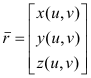
The direction of the normal at a point P is also given by the set of direction numbers

j₁, j₂, j₃

where j₁, j₂, j₃ are the Jacobians

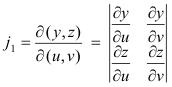
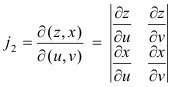
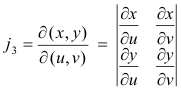
evaluated at point P. The surface is smooth at P if the three Jacobians do not vanish simultaneously there or, equivalently, if

Surface curves. We pose a question. How does one represent a curve on a surface? Let S be a simple surface element defined by the one-to-one mapping

x = x(u, v)

3) y = y(u, v)

z = z(u, v)

of a region R of the uv-plane into xyz-space. Let

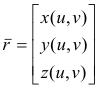
be the position vector to point P on the surface. How does one represent a curve on surface S? We do it as follows. We define a curve in the uv-plane by the parametric equations

4) u = u(t)

v = v(t) .

The mapping 3) then maps this curve onto the surface S. Substituting 4) into 3) gives us the equations of the curve as inscribed on surface S i.e.

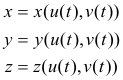
or, in vector form,

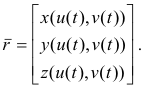
Surface curve tangents. Let S: be a simple surface element and let P be a point on S. Let at point P, where we are using subscripts to denote partial differentiation i.e.

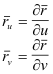
Let C be any curve on surface S passing through point P. Then the tangent vector to curve C at point P is given by

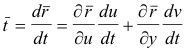
or, equivalently,

which shows that is a linear combination of the vectors and — which means that it lies in the same plane as and . Now the vectors and are tangent to the u- and v-coordinate curves at point P and define the surface tangent plane at point P. Thus we see that all surface curves passing through point P have, at point P, tangents which lie in the surface tangent plane there.

First and second fundamental quadratic forms of a surface. A space curve is completely determined by two local invariant quantities, curvature and torsion, as a function of arc length. In the same way a surface is completely determined by certain local invariant quantities called the first and second fundamental quadratic forms.

First fundamental quadratic form. Let S be a simple surface element defined by the one-to-one mapping

x = x(u, v)

y = y(u, v)

z = z(u, v)

of a region R of the uv-plane into xyz-space. Let

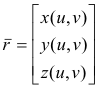
be the position vector to point P on the surface. The First Fundamental Quadratic Form is

where:

This form expresses the relationship between the differential of arc length ds for any curve on the surface S and the variables u, v, du and dv in the uv-plane. The quantities E, F and G are called the Fundamental Coefficients of the First Order of the surface. The form is positive-definite, meaning it is positive for all values of the variables.

Derivation

Theorem 2. At any point P on the surface S:

Proof.

Corollary. At any point P on the surface S: the unit surface normal is given by

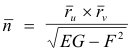
Second fundamental quadratic form. Let S be a simple surface element defined by the one-to-one mapping

x = x(u, v)

y = y(u, v)

z = z(u, v)

of a region R of the uv-plane into xyz-space. Let

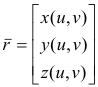
be the position vector to point P on the surface and let be the unit normal to the surface at point P. The Second Fundamental Quadratic Form is

6) ω = Ldu² + 2Mdudv + N dv²

where

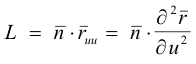
The quantities L, M and N are called the Fundamental Coefficients of the Second Order.

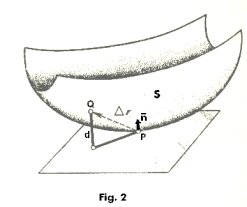
Physical interpretation of ω. Let P be the point corresponding to (u, v) and Q be the point corresponding to(u + du, v + dv) on surface S. See Fig. 2. Let d be the perpendicular distance from Q :(u + du, v + dv) to the plane tangent to S at P. Then d is equal to ½ω. Equation 6) gives ω as a function of the variables (du, dv) in a du-dv coordinate system. See Fig. 3.

Derivation

The values of d and ω can be either positive or negative, depending on the direction in which the unit surface normal is pointing. If is pointing in the direction of surface concavity then d and ω will be positive. Otherwise they will be negative. The direction in which points on a surface is something that is arbitrarily chosen, a matter of choice. Consulting Fig. 2, d is equal to PQ, which will be positive or negative depending on the direction of . In the figure is pointing in the direction of surface concavity and d is positive. The fact that the value of ω depends on can be seen from the fact that ω is a function of L, M and N which are dot products containing the vector .

Theorem. The quantities L, M, N are also given by

Proof.

Theorem 4. The Second Fundamental Quadratic Form is equal to i.e.

Proof.

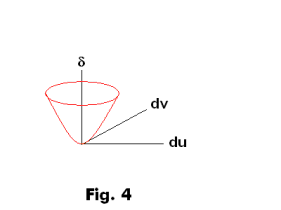
Osculating paraboloid at point P. The function

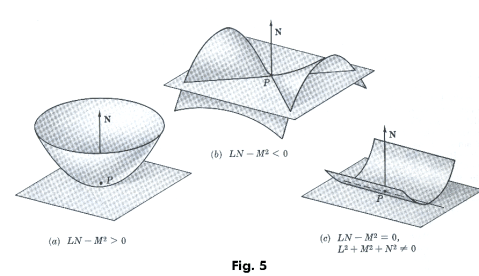
is called the osculating paraboloid at point P of the surface. The nature of this paraboloid determines the nature of the deviation of the surface from the tangent plane in the neighborhood of point P. If δ is plotted as a function of du and dv in a du-dv coordinate system (see figures 3 and 4) one will obtain one of four parabolic surfaces depending on the value the discriminate LN - M² of the quadratic form Ldu² + 2Mdudv + Ndv². See Fig 5.

Case 1. LN - M² > 0. Elliptic paraboloid. See Fig. 5(a). In this case the function represents a elliptic paraboloid and point P is referred to as an elliptic point. The surface lies completely on one side of the tangent plane.

Case 2. LN - M² < 0. Hyperbolic paraboloid. See Fig. 5(b). In this case the function represents a hyperbolic paraboloid and point P is called a hyperbolic point. Here there are two lines in the tangent plane passing through point P which divide the tangent plane into four sections in which δ is alternately positive and negative. See figure. On the two lines, δ = 0.

Case 3. LN - M² = 0 and the coefficients L, M and N are not all zero (i.e. L² + M² + N² ). Parabolic cylinder. See Fig. 5(c). In this case the function represents a parabolic cylinder and point P is called a parabolic point. Here there is a single line in the tangent plane passing through P along which δ = 0. Otherwise δ maintains the same sign.

Case 4. L = M = N = 0. Plane. In this case the degree of contact of the surface and the tangent plane is of higher order than in the other cases with the surface approximating a plane. Here point P is called a planar point.

Calculation of arc length, angles and surface area. The first fundamental coefficients E, F and G play a fundamental role in the calculation of arc length, angles and surface area on a simple surface element.

Arc length. Let S be a simple surface element defined by the one-to-one mapping

x = x(u, v)

8) y = y(u, v)

z = z(u, v)

of a region R of the uv-plane into xyz-space. Let

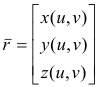
be the position vector to point P on the surface. Let

u = u(t)

v = v(t)

a t b define a curve in the uv-plane and let C be the image of this curve on surface S under mapping 8). A point on the curve is thus given by

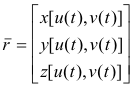
Length on curve C is then given by the integral

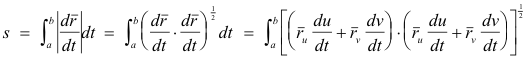
or, on expanding,

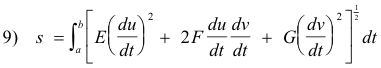
Angles between intersecting curves. Let two curves C₁ and C₂ issue from some point P on surface S with C₁ given by the equations

u = u₁(t)

v = v₁(t)

and C₂ given by the equations

u = u₂(t)

v = v₂(t) .

Then the tangents and to the two curves at point P are given by

Let be the angle between these two tangents. From the definition of a dot product it follows that

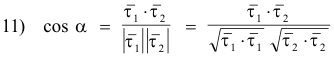
Substituting equations 10) into 11) we obtain

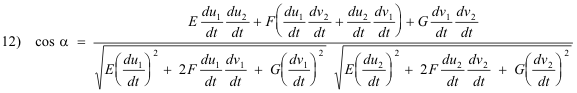
Angle between u-curves and v-curves. Let β be the angle between the u-curve and the v-curve at some point P. From the definition of a dot product it follows that

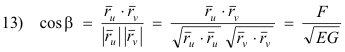
From 13) we have the following theorem:

Theorem. The u-curves and v-curves are perpendicular at a point if and only if F = 0.

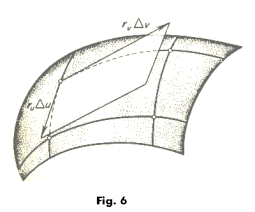
Surface area. To obtain a formula for area on a simple surface element we consider a curvilinear rectangle bounded by the coordinate curves u = u₀, v = v₀, u = u₀ + Δu, v = v₀ + Δv and use as an approximation to it the parallelogram lying in the tangent plane and bounded by the vectors tangent to the coordinate curves. See Fig. 6. The area of this parallelogram is