Functions, mappings, maps, transformations, operators. Onto, one-to-one, surjective, injective, bijective, identity, product, inverse functions. Group of transformations on a set. Permutation. Symmetric group Sn

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Functions, mappings, maps, transformations, operators. Onto, one-to-one, surjective, injective, bijective, identity, product, inverse functions. Group of transformations on a set. Permutation. Symmetric group Sn.

Def. Set. A finite or infinite collection of completely arbitrary objects.

Examples.

1) The set of numbers 1, 2, ... , n

2) The set of independent variables x₁, x₂, ... , x_n

3) The set of all points of a plane

4) The set of all triangles in the plane

5) The set of all rivers in China.

Def. Function (or mapping, map, transformation, operator). Suppose that to each element in a set A there is assigned, by some manner or other, a unique element of a set B. We call such assignments a function (or mapping, map, transformation, operator). If we let f denote these assignments, we write

which reads “f is a function of A into B”. The set A is called the domain of f and B is called the co-domain of f. If the function assigns b ε B to a ε A we say b is the image of a. The image of a is denoted by f(a), which reads “f of a”. It is called the value of f at a or the image of a under f . The element a is called the preimage of b. If P is any subset of A, then f(P) denotes the set of images of the elements of P; and if Q is any subset of B, then f ^-1(Q) denotes the set of elements of A which are mapped into Q. We call f(P) the image of P and f ^-1(Q) the inverse image or preimage of Q.

Syn. mapping, map, transformation, operator

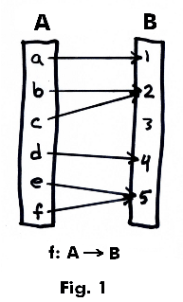
In a function from a set A into a set B, several elements of A may all image into the same element in B. In Fig. 1 elements a and b both image into 1. Also, the entire set B may not be covered. See Figure 1.

Range of a function. The range of a function consists of those elements of the co-domain that the function maps into. The co-domain consists of the entire set of elements being mapped into. In Fig. 1 the range consists of elements 1, 2, 3 and 5 whereas the co-domain consists of the entire set B. The range of

is denoted by f(A). Note that f(A) is a subset of B.

The objects of sets A and B can be quite arbitrary. Set A could represent integers, real numbers, complex numbers, vectors, matrices, functions, etc.. Likewise for set B.

Examples.

1] The area of a circle is a function of the radius; the sine of an angle is a function of the angle; the logarithm of a number is a function of the number. The expression y = 3x² + 7 defines y as a function of x where it is specified that the domain is (for example) the set of real numbers.

2] The matrix equation y = Ax where A is an mxn matrix and x and y are vectors from two different vector spaces defines a function from one vector space into another. The domain consists of vector space V and the co-domain consists of vector space W with x in V and y in W. Matrix A represents the function which can be viewed as an “operator” that operates on one vector to produce another.

3] The integral

is a function that assigns a real number to a real function f(x) defined on the interval [0,1].

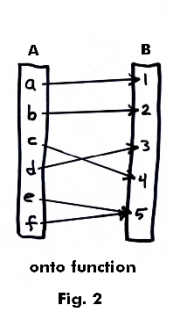
Onto function. A function is said to be “onto” if every element in co-domain B is the image of some element in domain A. Several elements of A may, however, map into the same element of B. See Figure 2.

Syn. surjective function, surjection.

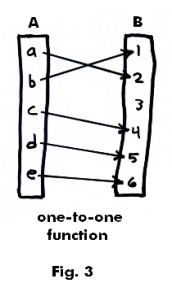
One-to-one function. A function is said to be “one-to-one” if every element of domain A maps into a different element of co-domain B. Different elements image into different elements. No two elements image into the same element. However, the whole set of B may not be covered. See Figure 3

Syn. injective function, injection.

Bijective function. A function that is both one-to-one and onto.

Equal functions. If f and g are functions defined on the same domain D and if f(a) = g(a) for every a D, then the functions f and g are equal and we write f = g.

Identity function. Let A be any set. Let the function f : A → A be defined by the formula f(x) = x, that is let f assign to each element in A the element itself. Then f is called the identity function or the identity transformation on A. It is the function I : A → A which leaves every point of A fixed.

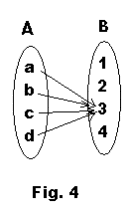
Constant function. A function f of A into B is called a constant function if the same element b B is assigned to every element in A. In other words, f: A → B is a constant function if the range of f consists of only one element. See Figure 4.

Example. Let f : R → R be defined by the formula f(x) = 3. Then f is a constant function since 3 is assigned to every element of the domain R.

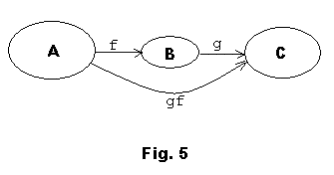
Product function. Let f be a function of A into B and let g be a function of B, the co-domain of f, into C. See Figure 5. Let a be an element in A. Then its image f(a) is in B which is the domain of g. Accordingly, we can find the image of f(a) under the mapping g, that is, we can find g(f(a)). Thus we have a rule which assigns to each element a A a corresponding element g(f(a)) C. In other words, we have a function of A into C. This new function is called the product function or composition function of f and g and is denoted by

(g f) or (gf)

More briefly, if f: A→ B and g: B → C then we define a function (g f): A → C by

(g f)(a) g(f(a))

Here ≡ is used to mean equal by definition.

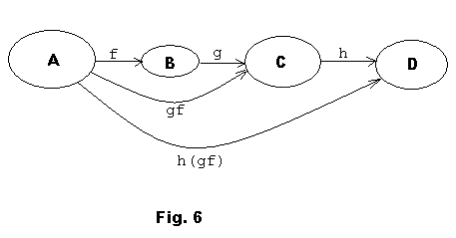
Associativity of products of functions. Let if f: A → B, g: B → C and h: C → D.

Then, as illustrated in Figure 6, we can form the product function gf: A → C and then the function h (gf): A → D.

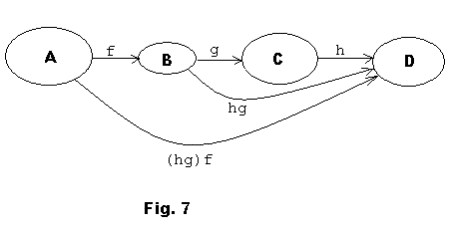
Similarly, as illustrated in Figure 7, we can form the product function hg: B → D and then the function (hg)f: A → D.

Both (h(gf) and (hg)f are functions of A into D. A basic theorem on functions states that these functions are equal.

Theorem. Let

f: A → B, g: B → C and h: C → D. Then

(hg)f = (hg)f

Thus multiplication of functions obeys the Associative Law for multiplication. As a consequence of this theorem we can write

hgf : A → D

without any parentheses.

Def. Inverse function. The function which exactly undoes the effect of a given function. Let f be a function of A into B and g be a function of B into A. Then g is an inverse of f if gf = I where I is the identity function. Thus g undoes the effect of f, leaving the set A unchanged. We denote the inverse of a function f by f ^-1. Thus if function f possesses an inverse f ^-1, then f ^-1f = I.

Existence of inverse functions. A function f may or may not have an inverse. We have seen that a function may assign the same image in B to several elements of A. See Figure 1 above. A function that does this cannot have an inverse. There is no function which will “undo” that kind of mapping. By definition, functions are single valued. For an inverse function to exist for a given function f the mapping must be one-to-one. In addition a mapping may not cover the entire co-domain. This causes an additional problem.

Mappings of a set into itself. Let G represent a mapping (or transformation) of a set S into itself. Every element a ∈ S is mapped into some element b ∈ S. Several elements of S may be mapped into the same element of S and, furthermore, not every element of S need be the image of some element of S. It can be seen that G is not necessarily either onto or one-to-one.

Examples of this kind of mapping are common in mathematics. Functions such as y = 5x³ and y = sin x represent mappings from the set of real numbers into the set of real numbers.

Let J(S) represent the set of all possible mappings of G on the finite set S = {a₁, a₂, ... , a_n). Then J(S) contains nⁿ elements since each element a_i ∈ S can be mapped onto any one of the n elements a₁, a₂, ... , a_n.

Every mapping G of a finite set S can be given by means of a table consisting of two rows with the upper row consisting of the names of the elements of S in an arbitrary order and the second row consisting of the images of the elements above them. For example

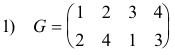
denotes the transformation of the set of numbers 1, 2, 3, 4 in which the numbers 1, 2, 3, 4 go over into the numbers 2, 4, 1, 3, respectively. The order of the elements in the top row is immaterial, however, and

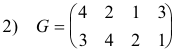
is equivalent to 1).

One-to-One transformations. Let Gʹ be a mapping that is both onto and one-to-one. Let O(S) represent the set of all possible mappings of Gʹ on set S = {a₁, a₂, ... , a_n). Then O(S) is a subset of J(S).

Theorem 1. O(S) is closed with respect to transformation multiplication.

Theorem 2. For a transformation T ∈ O(S) ,

TT^-1 =T^-1T = I

where I is the identity transformation.

Let us now consider an important concept, the concept of a group of transformations. The term “transformation” means the same as function. The terms are used interchangeably.

Def. Group of Transformations on a set S. Any set G of one-to-one transformations (i.e. functions) of a set S onto itself which meets the axiomatic conditions for being a group i.e.

1) Closure (if transformations f and g are in G, so is their product fg)

2) The associative law holds i.e. f(gh) = (fg)h

3) Existence of an identity element

4) Existence of inverses i.e. if transformation f is in G, so is its inverse f ^-1

Note that group G may be either a finite group or an infinite group. No stipulation on that is made.

Now consider the following important set: the set of all possible permutations of a set S of n objects onto itself. It meets all of the axiomatic requirements of a group.

Def. Permutation. An operation that replaces a set of n objects by one of its n! permutations.

Def. Symmetric group S_n on n letters. The group of all possible permutations on n objects.

References.

Lipschutz. Set Theory. Chap. 4

Lipchutz. Linear Algebra. p. 121

James and James. Mathematics Dictionary

Birkhoff, MacLane. A Survey of Modern Algebra. p. 119 - 123