Prove. The Divergence theorem. If V is the volume bounded by a closed surface S and A is a vector function of position with continuous derivatives, then
![]()
where n is the positive (outward drawn) normal to S.
Proof. The Divergence theorem in the full generality in which it is stated is not easy to prove. However given a sufficiently simple region it is quite easily proved.
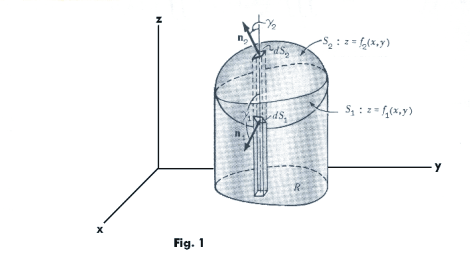
Let S be a closed surface so shaped that any line parallel to any coordinate axis cuts the surface in at most two points. We will now proceed to prove the following assertion:
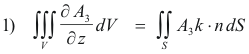
Denote the projection of the surface on the xy plane by R. A line erected from within R perpendicular to the xy plane intersects the surface at two points, at a lower surface and an upper surface. Denote the lower surface by S1 and the upper surface by S2. Let the equation of S1 be z = f1(x, y) and the equation of S2 be z = f2(x, y). See Fig. 1. Now

Now by the Fundamental Theorem of Integral Calculus
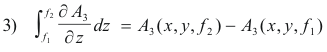
Substituting 3) into the right member of 2) we get
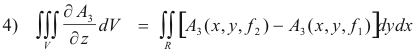
![]()
For the upper surface S2, dy dx = cos γ2 dS2 = k•n2 dS2 since the normal n2 to S2 makes an acute angle γ2 with k.
For the lower surface S1, dy dx = -cos γ1 dS1 = -k•n1 dS1 since the normal n1 to S1 makes an obtuse angle γ1 with k.
Consequently
![]()
![]()
Substituting 5) and 6) into 4) we get
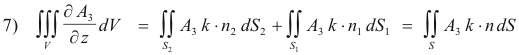
or
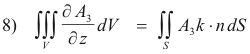
which is what we wished to prove.
In the same way, by projecting S on the other coordinate planes, we can obtain
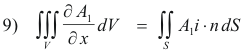
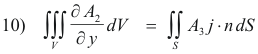
Adding 8), 9) and 10) we get
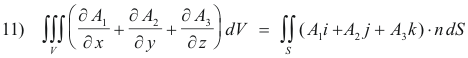
or
![]()
The theorem can be extended to surfaces which are such that lines parallel to the coordinate axes meet them in more than two points by subdividing the region into subregions whose surfaces do satisfy this condition. The procedure is similar to the one used in Green’s theorem in the plane.
References.
Spiegel. Vector Analysis.
Taylor. Advanced Calculus.