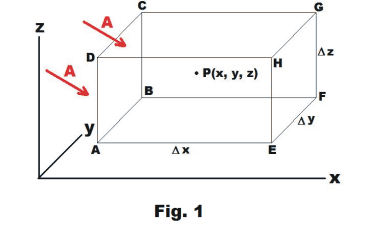
Prove. A fluid moves so that its flux at any point P(x, y, z) in some region R is given by A(x, y, z). Show that the gain of fluid per unit volume per unit time in a small parallelepiped having center at P(x, y, z) and edges parallel to the coordinate axes and having magnitudes Δx, Δy, Δz respectively, is given by div A = •A.

Proof. See Fig. 1. Denote the x component of flux A at point P by A₁(x, y, z). Then

Consequently,

Thus

Similarly,

Then

            total gain in volume per unit volume per unit time

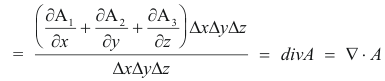
This is true exactly only in the limit as the parallelepiped shrinks to P i.e. as Δx, Δy and Δz approach zero.