Prove. is a vector perpendicular to the surface (x, y, z) = c where c is a constant.

Proof. Let r = xi + yj + zk be the position vector to any point P(x, y, z) on the surface. Then dr = dxi + dyj + dzk lies in the tangent plane to the surface at point P. Taking the total derivative of both sides of the equation

             (x, y, z) = c

gives

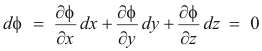
or

or

Thus is perpendicular to dr and therefore to the surface.

End of proof. 

Prove.

where

is the directional derivative of (x, y, z) in the direction of unit vector a.

Proof. In calculus we learn that the directional derivative of a function (x, y, z) in the direction of a unit vector a is given by

where α, β and γ are the direction cosines of the unit vector a. It follows immediately that