Similarity, Similar matrices, Orthogonal similarity, Real quadratic forms, Hermitian matrices, Normal matrices

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Similarity, Similar matrices, Diagonable matrices, Orthogonal similarity, Real quadratic forms, Hermitian matrices, Normal matrices

Similar matrices. Two n-square matrices A and B over a field F are called similar if there exists a non-singular matrix P over F such that

(1) B = P^-1AP

Note. Note that if B = P^-1AP then A = PBP^-1 . The condition of similarity can be defined by either formula. The formula B = P^-1AP becomes B = QAQ^-1 if we let Q = P^-1.

Similarity is an equivalence relation that separates the set of all n-square matrices into equivalence classes. All matrices similar to a given matrix are similar to each other. What is the significance of this relationship of similarity between matrices? The answer is that any matrix similar to a given matrix represents the same linear transformation as the given matrix, but as referred to a different coordinate system (or basis). Thus any two matrices that are similar to each other represent the same point transformation in n-space i.e. they map points in the same way, they represent the same linear point transformation.

The concept of similarity is thus intricately connected to the concept of a change in basis, a change in coordinate system. Changing the basis for a linear transformation produces similar matrices.

Changes in the expression of a linear transformation due to a change in basis. Let Y = AX be a linear point transformation expressed with respect to the E-basis. What is the expression for this same transformation when expressed with respect to some arbitrary other Z-basis? In the Z-basis the vectors X and Y are

X = ZX_Z Y = ZY_Z .

Substituting into Y = AX we get

ZY_Z = AZX_Z

Y_Z = Z^-1AZX_Z .

Thus we see that the matrix Z^-1AZ of the point transformation with respect to the Z-basis is similar to the matrix A of the transformation with respect to the E-basis.

All matrices that are similar to each other represent the same linear point transformation, but as referred to different frames of reference, or basis. Of great importance are those n-square matrices that are similar to diagonal matrices. Any matrix that is similar to a diagonal matrix represents the same linear point transformation as the diagonal matrix. What are the characteristics of the linear point transformation effected by a diagonal matrix? The answer is as follows.

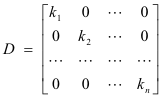
Point transformation effected by a diagonal matrix. The point transformations effected by a diagonal matrix represent a very important class of linear transformations. Given the diagonal matrix

consider the point transformation effected by it in n-space (i.e. the transformations given by Y = DX ). The transformations of this class have a very simple and intuitive geometric meaning (of course, only for two and three-dimensional real spaces). If the numbers k_i are all positive the effect of this transformation is simply stretching (or compressing) effects directed in the directions of the different coordinate system axes e₁, e₂, .... ,e_n with magnitudes given by k₁, k₂, .... ,k_n. If some of the k_i are negative, then the deformation of the space is accompanied by a change of direction. Finally, if for example k₁= 0, then a projection of the space parallel to e₁ takes place onto the subspace spanned by e₂, e₃, .... ,e_n with a subsequent deformation in these directions. If the coordinate system is an oblique one the transformation will transform figures in space in this linear way in the directions of the oblique axes.

This class of transformations is important because in spite of its simplicity it is very general. In fact, it can be established that every linear transformation satisfying certain not very severe restrictions belongs to this class i.e. we can find for it a basis in which it is described by a diagonal matrix. [ excerpted from Mathematics, Its Content, Methods and Meaning. Vol. III. p. 80]

Diagonable matrices. A mattrix A which is similar to a diagonal matrix is called diagonable.

Under what conditions is an n-square matrix similar to a diagonal matrix? The following theorems address that question.

Theorems.

1] If all the eigenvalues of a matrix are distinct, then the matrix is similar to a diagonal matrix whose diagonal elements are these eigenvalues.

2] If an n-square matrix has n linearly independent eigenvectors, it is similar to a diagonal matrix.

3] An n-square matrix A is similar to a diagonal matrix if and only if the eigenvectors of A span V_n(F); when this is the case, the eigenvalues of A are the diagonal elements of D.

4] An n-square matrix A is similar to a diagonal matrix if and only if for each eigenvalue λ_i of A, the multiplicity of λ_i is equal to the dimension of the null space of λ_iI - A.

5] Two diagonal matrices are similar if and only if they differ only in the order of their diagonal elements.

6] Let A be an n-square matrix with n linearly independent eigenvectors p₁, p₂, ... , p_n and let λ₁, λ₂, ... , λ_n be the eigenvalues corresponding to p₁, p₂, ... , p_n. Let P be a matrix whose columns 1, 2, ... , n consist of p₁, p₂, ... , p_n i.e.

P = [p₁ p₂ ... p_n]

and let D be the diagonal matrix

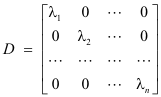
whose diagonal elements consist of the eigenvalues λ₁, λ₂, ... , λ_n. Then matrix P is non-singular and

2) A = PDP^-1

or, equivalently,

3) D = P^-1AP .

Proof of Theorem 6].

Significance of Theorem 6. What is the significance of Theorem 6? Consider the linear point transformation

Y = AX

where matrix A has n distinct eigenvalues and thus also n corresponding linearly independent eigenvectors. We would like to know something about the nature of this linear point transformation effected by matrix A, just how it transforms figures in n-space. Could we perhaps get some insight into how it transforms figures by doing a change of coordinate system, transferring over to the coordinate system defined by the eigenvectors? Let us do a change of coordinate system, a change of basis, transferring over to the eigenvector coordinate system. From Theorem 6 we know that if Y = AX then Y = PDP^-1X where P is a matrix whose columns consist of the eigenvectors and D is a diagonal matrix whose diagonal elements consist of the corresponding eigenvalues. If X' and Y' are the values of X and Y in the eigenvector coordinate system the equations relating the coordinates in the two systems are

X = PX'

Y = PY' .

Substituting into Y = PDP^-1X we get

PY' = PDP^-1PX'

or, equivalently,

4) Y' = DX' .

Thus in the eigenvector coordinate system the linear point transformation Y = AX is given by Y' = DX' , a transformation effected by the diagonal matrix D. What does this tell us? It tells us that the transformation of the figure by Y = AX consists of a distortion consisting of stretching (or compressing) in the directions of the various eigenvector axes by amounts given by the associated eigenvalues. It gives us an intuitive insight into the linear point transformation Y = AX.

Similar matrices and eigenvalues.

7] Two similar matrices have the same eigenvalues.

Relationship between the eigenvectors of two similar matrices. Let X_i be an eigenvector of a matrix A corresponding to an eigenvalue λ_i of A. Then an eigenvector Y_i of a similar matrix B = P ^-1AP corresponding to the same eigenvalue λ_i of B is given by Y_i = P^-1X.

Eigenvalues and eigenvectors of diagonal matrices.

8] The eigenvalues of a diagonal matrix D = diag(a₁, a₂, .... ,a_n) are simply the diagonal elements.

9] A diagonal matrix D = diag(a₁, a₂, .... ,a_n) always has n linearly independent eigenvectors. The elementary unit vectors

..................

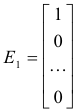
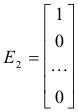
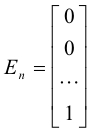
constitute a set of n linearly independent eigenvectors for D since DE_i = a_iE_i, ( i =1, 2, ...., n).

General theorems.

10] Any n-square matrix A, similar to a diagonal matrix, has n linearly independent eigenvectors.

11] Every square matrix A is similar to a triangular matrix whose diagonal elements are the eigenvalues of A.

12] If A is any real n-square matrix with real eigenvalues, there exists an orthogonal matrix Q such that Q ^-1AQ = Q^TAQ is triangular and has as diagonal elements the eigenvalues of A The matrices A and Q ^-1AQ are called orthogonally similar.

13] If A is any n-square matrix with complex elements or a real n-square matrix with complex eigenvalues, there exists a unitary matrix U such that is triangular and has as diagonal elements the eigenvalues of A. The matrices A and are called unitarily similar.

Synonyms.

Eigenvalue, characteristic root, latent root

Eigenvector, characteristic vector, invariant vector, latent vector

Eigenvector space, characteristic vector space, invariant vector space

Real symmetric matrices.

1] The characteristic roots (i.e. eigenvalues) of a real symmetric matrix are all real.

2] The invariant vectors (i.e. eigenvectors) associated with distinct characteristic roots of a real symmetric matrix are mutually orthogonal.

3] If A is a real n-square symmetric matrix with characteristic roots λ₁, λ₂, ... , λ_n, then there exists a real orthogonal matrix P such that P^TAP = P^-1AP = diag(λ₁, λ₂, ... , λ_n).

4] If λ_i is a characteristic root of multiplicity r_i of a real symmetric matrix, then there is associated with λ_i an invariant space of dimension r_i .

Orthogonal similarity. If P is an orthogonal matrix and B = P^-1AP. then B is said to be orthogonally similar to A. Since P^-1 = P^T, B is also orthogonally congruent and orthogonally equivalent to A.

Every real symmetric matrix A is orthogonally similar to a diagonal matrix whose diagonal elements are the characteristic roots of A.

Canonical set for real symmetric matrices under orthogonal similarity. Let the characteristic roots of the real symmetric matrix A be arranged so that λ₁ ≥ λ₂ ≥.... ≥ λ_n . Then diag( λ₁, λ₂, ... , λ_n) is a unique diagonal matrix similar to A. The totality of such diagonal matrices constitutes a canonical set for real symmetric matrices under orthogonal similarity.

Two real symmetric matrices are orthogonally similar if and only if they have the same characteristic roots, that is if and only if they are similar.

Real quadratic forms.

1] Every real quadratic form q = X^TAX can be reduced by an orthogonal transformation X = BY to a canonical form

where r is the rank of A and λ₁, λ₂, ... , λ_n are its non-zero characteristic roots.

2] A real symmetric matrix is positive definite if and only if all of its characteristic roots are positive.

3] If X^TAX and X^TBX are real quadratic forms in (x₁, x₂, .... ,x_n) and if X^TBX is positive definite, there exists a real non-singular linear transformation X = CY which carries X^TAX into

and X^TBX into

where λ_i are the roots of |λB - A| = 0 .

Hermitian matrices.

1] The characteristic roots of an Hermitian matrix are real.

2] The invariant vectors associated with distinct characteristic roots of an Hermitian matrix are mutually orthogonal.

3] If H is an n-square Hermitian matrix with characteristic roots λ₁, λ₂, ... , λ_n, there exists a unitary matrix such that = diag(λ₁, λ₂, ... , λ_n ) . The matrix H is called unitarily similar to .

4] If λ_i is a characteristic root of multiplicity r_i of the Hermitian matrix H, then there is associated with λ_i an invariant space of dimension r_i .

Canonical set for Hermitian matrices under unitary similarity. Let the characteristic roots of the Hermitian matrix H be arranged so that λ₁ ≤ λ₂ ≤ .... λ_n. Then diag(λ₁, λ₂, ... , λ_n) is a unique diagonal matrix similar to H. The totality of such diagonal matrices constitutes a canonical set for Hermitian matrices under unitary similarity.

Two Hermitian matrices are unitarily similar if and only if they have the same characteristic roots, that is if and only if they are similar.

Normal matrices. An n-square matrix A is called normal if . Normal matrices include diagonal, real symmetric, real skew-symmetric, orthogonal, Hermitian, skew-Hermitian and unitary matrices.

1] If is a normal matrix and is a unitary matrix, then is a normal matrix.

2] If X_i is an invariant vector corresponding to the characteristic root λ_i of a normal matrix A, then X_i is also an invariant vector of corresponding to the characteristic root .

3] A square matrix A is unitarily similar to a diagonal matrix if and only if A is normal.

4] If A is normal, the invariant vectors corresponding to distinct characteristic roots are orthogonal.

5] If λ₁ is a characteristic root of multiplicity r_i of a normal matrix A, the associated invariant space has dimension r_i .

6] Two normal matrices are unitarily similar if and only if they have the same characteristic roots, that is if and only if they are similar.

References.

1. Ayres. Matrices (Schaum).

2. Mathematics, Its Content, Methods and Meaning. Vol. III