Website owner: James Miller
Hermitian forms, Equivalence, Conjunctive Hermitian matrices, Reduction to canonical form, Definite and semi-definite forms
Hermitian Form. The form in n variables defined by
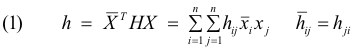
where matrix H is n-square and Hermitian and the components of vector X are complex numbers. The rank of H is called the rank of the form. If the rank r is less than n the form is called singular. If the rank is equal to n it is non-singular. The value h of a Hermitian form is always real.
If H and X are real, the Hermitian form reduces to the quadratic form as a special case.i.e. if H and X are real, (1) above is a real quadratic form. As a consequence, the theorems for Hermitian forms are analogous to those for quadratic forms.
Hermitian forms arise in different places, including atomic physics.
Linear transformations on Hermitian forms. The non-singular linear
transformation X = BY carries the Hermitian form
into another Hermitian form
.
Equivalence of Hermitian forms. Two Hermitian forms are said to be equivalent if and only if there exists a non-singular linear transformation X = BY that carries one of the forms into the other.
Conjunctive Hermitian matrices. Two n-square Hermitian matrices A and B are
called congunctive if there exists a non-singular matrix P such that
.
Two Hermitian forms are equivalent if and only if their matrices are conjunctive.
The rank of an Hermitian form is invariant under a non-singular transformation of the variables.
Reduction to canonical form. A Hermitian form
of rank r can be reduced to
the canonical form
of index p and signature p - (r - p) .
Two Hermitian forms are equivalent if and only if they have the same rank and the same index or the same rank and the same signature.
Definite and semi-definite forms.
Positive definite form. A nonsingular Hermitian form h =
in n variables is
called positive definite if its rank and index are equal. Because it is nonsingular its rank r is
equal to n. Thus, a positive definite Hermitian form can be reduced to
. Its value h is greater than zero for any value of the X’s except the
trivial case
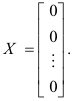
Positive semi-definite form. A singular Hermitian form h =
in n variables is
called positive semi-definite if its rank and index are equal. Because it is singular its rank r is
less than n. Thus, a positive semi-definite Hermitian form can be reduced to
where r < n. Its value h is greater than or equal to zero for any value of
the X’s.
Definite and semi-definite matrices. The matrix H of an Hermitian form
is called positive definite or positive semi-definite according as the Hermitian form is positive definite or positive semi-definite.
An Hermitian form is positive definite if and only if there exists a nonsingular matrix C such that
.
If an Hermitian matrix H is positive definite, every principal minor of H is positive, and conversely.
If an Hermitian matrix H is positive semi-definite, every principal minor of H is non-negative, and conversely.
References.
Ayres. Matrices (Schaum).
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life