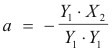
Derivation of Gram-Schmidt orthogonalization procedure. Suppose X₁ , X₂ , ..... , X_m constitute a basis of some vector space. We wish to devise a procedure for generating from these m vectors an orthogonal basis for the space. Denote by Y₁ , Y₂ , ..... , Y_m the set of mutually orthogonal vectors to be found.

1) Let Y₁ = X₁

2) Let Y₂ = X₂ + aY₁ .

Since Y₁ and Y₂ are to be mutually orthogonal we specify the condition

            Y₁·Y₂ = Y₁· (X₂ + aY₁ ) = Y₁·X₂ + Y₁ · aY₁ = Y₁ · X₂ + a Y₁·Y₁ = 0

Consequently,

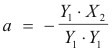
and

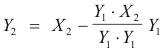
3) Let Y₃ = X₃ + aY₂ + bY_{1 .}

Since Y₁ , Y₂ and Y₃ are to be mutually orthogonal we specify the conditions

            Y₁·Y₃ = Y₁· (X₃ + aY₂ + bY₁ ) = Y₁·X₃ + aY₁ · Y₂ + bY₁ · Y₁ = Y₁ · X₃ + b Y₁·Y₁ = 0

and

            Y₂·Y₃ = Y₂· (X₃ + aY₂ + bY₁ ) = Y₂·X₃ + aY₂· Y₂ + bY₂· Y₁ = Y₂ · X₃ + a Y₂·Y₂ = 0

Consequently,

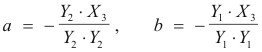
and

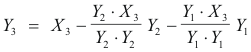
4) Continue process until Y_m is obtained.