Prove. A system AX = B of m linear equations in n unknowns is consistent if and only if the coefficient matrix and the augmented matrix of the system have the same rank.

Proof. We shall show in a heuristic way why the above assertion must be true. The rank of a matrix is equal to the number of linearly independent rows that it contains. We shall show that in order for a solution to exist (i.e. for the system to be consistent) the number of linearly independent rows in the coefficient matrix must be equal to the number of linearly independent rows in the augmented matrix.

First we note that if a linear system is inconsistent it is because it contains a set of contradictory equations, equations such as

            3x + 5y + 2 z = 9

            3x + 5y + 2 z = 11,

although the fact of their conflict may be disguised and not evident until the system is reduced to simplified standard form through elementary row operations.

Suppose we have a set of m equations in three unknowns

            a₁x + b₁ y + c₁z = d₁

            a₂x + b₂ y + c₂z = d₂

            .....................

            a_mx + b_m y + c_mz = d_m

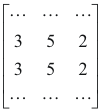
and it contains the above two contradictory equations. Then the coefficient matrix will contain the row (3 5 2) twice i.e. the matrix will look like

Thus these entries in the coefficient matrix represent two identical, linearly dependent rows. On the other hand in the augmented matrix these rows appear as

which are two linearly independent rows. Thus the existence of a set of contradictory equations in a linear system causes the coefficient matrix to have one less independent row than the augmented matrix (i.e. it causes the count of independent rows in the coefficient matrix to be one less than in the augmented matrix). If there are no sets of contradictory equations in the system the number of independent rows in the coefficient matrix and the augmented matrix will be the same.