Website owner:  James Miller

Determinant, Minor, Cofactor, Evaluation of a determinant by cofactors

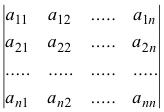
Determinant. A square array of quantities, called elements, symbolizing the sum of certain products of these elements. The symbol

denotes a determinant of order n. It is an abbreviation for the algebraic sum of all possible products

where each product of n factors contains one and only one element from each row and one and only one element from each column. There will be n! such products. Each product has a plus or minus sign attached to it according as the column indices form an even or odd permutation when the row indices are in natural order (i.e. 1, 2, 3, ... ) .For example, the term of the expansion of a determinant of order four has the column indices in order (3,1,4,2) . This term should have a negative sign attached, since three successive interchanges will change the column indices to (1,3,4,2), (1,3,2,4) and (1,2,3,4), the last being in natural order.

Properties of determinants.

1. If all the elements of a column (or row) are zero, the value of the determinant is zero.

2. If each of the elements in a row (or column) of a determinant is multiplied by the same number p, the value of the determinant is multiplied by p.

3. If two columns (or rows) are identical, the value of the determinant is zero.

4. Interchanging any two rows (or columns) reverses the sign of the determinant.

5. The value of a determinant is unaltered when all the corresponding rows and columns are interchanged i.e. for a square matrix ,

Thus any theorem proved true for rows holds for columns, and conversely.

Example.

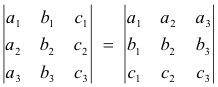
6. If each element of a row (or column) of a determinant is expressed as the sum of two (or more) terms, the determinant can be expressed as the sum of two (or more) determinants.

Example.

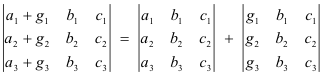
7. If to each element of a row (or column) of a determinant is added m times the corresponding element of another row (or column) the value of the determinant is not changed.

Minor of an element in a determinant. The determinant, of next lower order, obtained by striking out the row and column in which the element lies.

Cofactor of an element in a determinant. Denote the minor of element a_ij of the i-th row and j-th column of a determinant |A| by |M_ij |. The cofactor of the element a_ij is given as the signed minor (-1)^i+j |M_ij | i.e. it is the minor, taken with a positive or negative sign, according as the sum of the column number and the row number is even or odd.

Example. Let

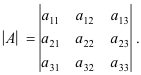
Then the minor of element a₂₁ is

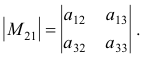
The cofactor of element a₂₁ is

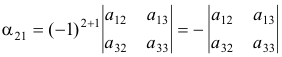
Evaluation of a determinant by minors. The value of a determinant of order n is equal to the sum of the products formed by multiplying each element of any selected row (or column) by its cofactor. The value of a determinant of order 1 is the value of the single element of the determinant.

Example. Let

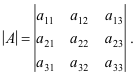
Then

where a₁₁, a₁₂ and a₁₃ are the cofactors of a₁₁, a₁₂ and a₁₃.

*************************************

Minors and cofactors of matrices

*************************************

Minor of an element of a square matrix. The minor of an element a_ij of an n-square matrix is the determinant of the (n-1)-square matrix obtained by striking out the row and column in which the element lies.

Cofactor of an element in a square matrix. Denote the minor of element a_ij of the i-th row and j-th column of a matrix A by |M_ij | . The cofactor of the element a_ij is given as the signed minor (-1)^i+j |M_ij | i.e. it is the minor, taken with a positive or negative sign, according as the sum of the column number and the row number is even or odd.