Website owner: James Miller
Prove. The torque L on a coil of n turns carrying a current I in a magnetic field B is
1) L = nBIA sin θ

where A is the area inclosed by a single turn or loop of the coil and θ is the angle between the normal to the loop and the magnetic field B.
Proof. We will consider three cases: 1) A rectangular loop, 2) A circular loop , and 3) A solenoid.
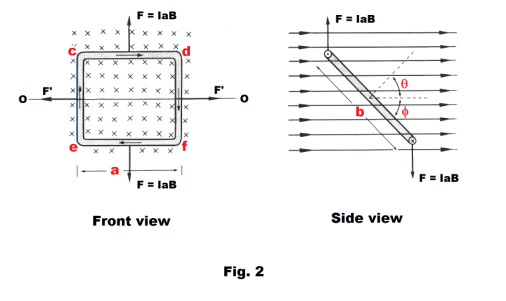
Rectangular loop. Fig. 1 shows a rectangular loop of wire of dimensions a by b carrying a current I. Fig. 2 shows the front and side views of the same loop, minus the leads going in and out of the loop for simplicity. The loop is pivoted on an axis OO that is perpendicular to the direction of a uniform magnetic field B. The normal to the plane of the loop makes an angle θ with the direction of the field as shown in the side view. Sides cd and ef are thus perpendicular to the field. Using the formula F = BIs sin θ for the force exerted on a long straight conductor by a magnetic field, we see that an upward force of F = IaB is exerted on side cd and a downward force of F = IaB is exerted on side ef. Sides ce and df make an angle f with the field. A force of F' = IbB sin f is exerted to the left on ce and an equal force is exerted to the right on df. The resultant force on the loop in the x, y and z directions is zero, however, there is a torque on the loop since the forces on sides cd and ef constitute a couple of moment
2) L = IaB ∙ b sin θ
The area A of the loop is given by A = ab, so 2) becomes
3) L = BIA sin θ
If the coil is a closely wound one with n turns, then
3) L = nBIA sin θ
The couple is a maximum when θ = 90o, or when the plane of the coil is parallel to the field, and is zero when θ = 0, or when the plane of the coil is perpendicular to the field.
Circular loop. If we replace a circular loop by a very large number of small rectangular loops, the sum of the area of the rectangular loops can be made to approach the area of the circular one as closely as we wish and the boundary of the rectangular loops can be made approach the boundary of the circular loop as closely as we wish. Currents in the same direction in all the rectangular loops will give rise to forces that cancel at all points except on the boundary. It can be shown that, not only for a circular loop, but for a loop of any shape carrying a current I in a field of flux density B, the torque is given by
L = nBIA sin θ
Solenoid. If a solenoid is closely wound, it can be approximated by a number of circular turns lying in planes at right angles to its long axis. The total torque acting on a solenoid is simply the sum of the torques on the individual turns. Consequently, for a solenoid of n turns in a uniform field of flux density B,
L = nBIA sin θ