Website owner: James Miller
Voltaic cells. Flow of electric current. Electromotive force. Electrical resistance. Ohm’s law. Resistivity. Temperature and resistivity. Current density. Drift velocity.

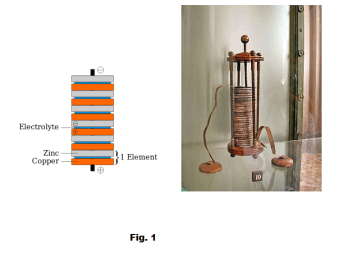
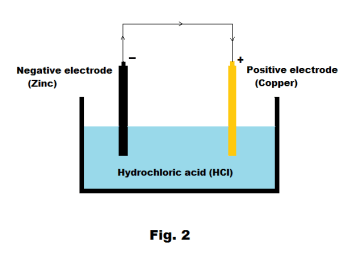
Voltaic cells. The first device to produce a steady, lasting electric current was the voltaic cell invented by Italian physicist Alessandro Volta. He created a voltaic pile in 1800 by stacking alternating copper and zinc disks separated by disks of cardboard soaked in saltwater. See Fig. 1. When the top and bottom disks were connected by a wire an electric current (i.e. a stream of electrons) would flow through the wire. Fig. 2 shows a voltaic cell consisting of a zinc rod and copper rod sitting in a solution of HCl. This cell will develop a potential difference of about 1.5 volts. A current (a stream of electrons) will flow from the negative zinc terminal to the positive copper terminal if the terminals are connected by a wire.
Flow of electric current. The flow of an electric current in a wire is analogous to the flow of water in a pipe. The rate at which water flows through a pipe is given as the number of gallons (or cubic feet, or whatever) passing a particular point in the pipe per second. In the same way, the rate at which current flows in a wire is given as the number of coulombs of charge that passes through a cross-section of the wire per second. The rate of flow of current in a wire is given in amperes where one ampere represents a flow of one coulomb of charge per second. Thus if the flow rate of current at some point in a wire is three amperes, it means that three coulombs of charge is flowing past the point per second. Although an ampere represents a current flow of one coulomb per second, its official definition is as follows:
Def. Ampere. That constant current which, if present in each of two parallel conductors of infinite length and one meter apart in empty space, causes each conductor to experience a force of exactly 2 × 10–7 newton per meter of length.
One coulomb of charge is approximately 6.3 billion billion electrons. And that is about the amount of charge that flows through a 100-watt filament lamp every second. However, because so many electrons pass a point in a second doesn’t mean that electrons speed down a wire at lightening speed. To the contrary, at a flow rate of one ampere, the electrons are only moving down the wire at a speed of about 0.001 mm/sec. The reason that a light goes on the second the switch is closed is not because the electrons race around it at high speed, but because the conductors are always “filled” with electrons, just as a pipe system is always full of water. The electric field in the wire moves at the speed of light, but the electrons move slowly.
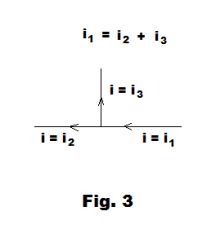
Electron flow in a wire behaves like the flow of an incompressible liquid (like water in a pipe) and this means that the electrons cannot accumulate anywhere. If they are set in motion at any point in a series circuit, they are nearly simultaneously set in motion at every point in the circuit. It also means that at every branch point, or junction, in a circuit, the sum of the currents which leave the junction must total up to the sum of all the currents entering the junction. Thus, for the currents i1, i2 , and i3 shown in Fig. 3, i1 = i2 + i3.
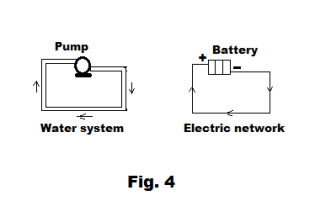
An electrical network is similar to a water system in the following way also: The purpose of the circulating pump in a water system is to maintain a pressure difference between its inlet and outlet in order to keep the water circulating. The purpose of a battery in an electrical network is to maintain an electrical potential difference between its two terminals in order to keep the current flowing in the circuit. See Fig. 4.
Note on terminology. It is customary to say that the current (or “current intensity” or “current strength”) in a wire is, say, 5 amperes. What we really mean is that the rate of flow of the current is 5 amperes, or 5 coulombs per second. There is some imprecision or ambiguity in the language. A large river flowing at a rate of one inch per second may have the same flow rate as a small stream flowing at a rate of 10 feet per second. The size of a stream is thus not conceptually equivalent to its flow rate.
If q coulombs of charge pass through a cross-section of a wire in t seconds, then the current I in the wire is given by
I = q/t
Sources of continuous current. We list the following sources of continuous current:
1. Electrochemical cells. Electrochemical cells produce electricity through chemical reactions. Electrochemical cells include primary cells, storage cells, and fuel cells. A primary cell is an electrochemical cell that generates an electric current by an irreversible chemical reaction and is designed to be used and then discarded. Primary cells include the voltaic cell and the dry cell. Storage cells are electrochemical cells that employ reversible chemical reactions that make the cells rechargeable. An example is the lead-acid automobile battery. A fuel cell is a device that converts the chemical energy from a fuel (such as hydrogen or methanol) into electricity through a chemical reaction with oxygen or some other oxidizing agent.
2. Solar cells. A solar cell converts visible light into electrical current. It is based on the ability of certain semiconductor materials to generate small amounts of electric current when exposed to light. When light strikes the solar cell, electrons are knocked loose from the atoms of the semiconductor material. If the two sides of the solar cell are connected by a wire, an electric current will flow.
3. Thermocouples. If wires of two dissimilar metals (such as copper and iron) are joined at their ends, and these ends are maintained at different temperatures, a current will flow in the wires. A thermocouple is a device based on this fact. The voltage of the thermocouple depends on the two metals used and on the difference in temperature.
4. Piezoelectric effect. When certain crystals, such as Rochelle salt and quartz, are subjected to a mechanical stress, the opposite surfaces become electrically charged, the potential difference generated between the sides being proportional to the amount of stress applied. If the two sides are connected by a wire, current will flow. This is known as the Piezoelectric effect.
5. The electric generator. The operation of an electric generator is based on the fact that if a conducting loop is rotated in a magnetic field, an electric current will flow in the loop by a mechanism called electromagnetic induction.
Def. Electromotive force (emf). The potential difference, or voltage, developed by any source of electrical energy such as a voltaic cell, storage battery, electrical generator, solar cell, thermocouple, piezoelectric cell, etc.
A source of emf can be thought of as a kind of charge pump that moves charge through its interior from a point of low potential to a point of high potential. The source of emf, by chemical, mechanical or other means, performs work on that charge to move it to the high potential terminal. The emf of the source is defined as the work done per unit charge in moving a small test charge from the point of low potential to the point of high potential i.e. if dW is the work done in moving test charge dq from the point of low potential to the point of high potential, then the emf E is given by
1) E = dW/dq.
Emf is measured by the potential difference between the terminals when the battery or generator is not delivering current. In the mks system, the unit of emf is the volt (1 joule per coulomb).
A source of emf is often called a seat of emf.
Electrical resistance. Just as the pipes in a water system offer some resistance to the passage of water due to friction, in the same way even the best conductors of electricity offer some resistance to the passage of electrons. If a conductor did not offer resistance to the motion of electrons, the electrons would accelerate under the influence of the electric field and their velocity would continually increase with no limit, resulting in an ever increasing rate of flow of the current. This doesn’t happen. The rate of flow of the current remains constant as long as the electric field is constant. This can be explained by assuming that after a momentary acceleration, an electron collides with one of the fixed particles in a conductor and is slowed down or stopped, after which it again accelerates, etc. In this way it moves with a certain average velocity, called the drift velocity, which for a flow rate of one ampere is a speed of about 0.001 mm/sec. The collisions with the fixed particles result in a transfer of energy to them which increases their energy of vibration and results in the development of heat.
We know that for the case of water flowing in a pipe, the flow rate will increase if the water pressure is increased. Also, the flow rate will decrease if the resistance offered by the pipe increases. We might wonder if the same might occur with electricity. We might suspect that the flow rate of an electric current would increase with increased potential difference and decrease if the resistance of the circuit is increased. In fact, it does. Georg Simon Olm (1787 - 1845), a German physicist, investigated these questions and in his book, The Galvanic Circuit Investigated Mathematically) (1827), and gave the following law:
Ohm’s law. The potential difference Vab between any two points a and b in a circuit is related to the current I and the resistance R in that part of the circuit by
![]()
Here the unit of resistance, ohms, is defined implicitly by 2), in terms of amperes and volts:
Def. Ohm. The resistance between two points of a conductor when a constant potential difference of 1.0 volt, applied to these points, produces in the conductor a current of 1.0 ampere.
The Greek letter Ω is used as a symbol for ohms. Thus 3.2 ohms can be written 3.2 Ω.
Factors affecting resistance. There are several factors which affect the resistance of a conductor:
1] Length. The resistance of a conductor is directly proportional to its length. If one foot of water pipe offers a certain amount of resistance to water flowing through it, ten feet of pipe will offer ten times as much resistance. The same is true for electricity flowing in a conductor.
2] Cross-sectional area. The resistance of a conductor is inversely proportional to its cross-sectional area. The larger the diameter, the less the resistance.
3] Temperature. The resistance of a metallic conductor increases with its temperature.
4] Material. The resistance depends on the material.
The resistance of a conductor is given by the formula
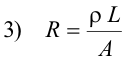
where:
ρ = a constant, called the resistivity, that depends on the material and the temperature
L = length of the conductor
A = cross-sectional area of the conductor
Resistivity. If a conductor is of unit length and unit cross sectional area, L/A = 1 in formula 3) and ρ = R. Consequently, the resistivity can be viewed as the resistance of a specimen of the material of unit length and unit cross-sectional area.
In the mks system, where the unit of length is the meter and the unit of area is the square meter, the resistivity ρ is equal to the resistance, in ohms, between opposite sides of a cube of the material measuring one meter on a side. Resistivities are expressed in ohm-meters.
If the centimeter is used as a unit of length and the square centimeter as a unit of area, the resistivity ρ is equal to the resistance of a wire 1 cm long and having a uniform cross-sectional area of 1 cm2. Resistivities are expressed in ohm-centimeters.
The resistivity of a pure metal in a definite crystalline state and at a definite temperature is a quantity characteristic of the metal. However, impurities in the metal (even in small quantities) or changes in the crystalline structure due to heat treatment or mechanical strain, can have a pronounced effect on the resistivity. For example, the resistivity of commercial annealed copper at 20o C is 1.72×10-8 ohm-m and that of hard drawn copper is 1.77×10-8 ohm-m.
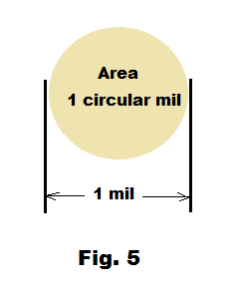
Computing wire resistance in the English system. In the English system the cross-sectional area of round wire is expressed in circular mils.
Def. Mil. A mil equals 0.001 inch.
Def. Circular mil. A circular mil is a unit of area, equal to the area of a circle with a diameter of one mil. See Fig. 5.
The area A, expressed in circular mils, of a circle with a diameter of d mils, is given by the formula
A = d2.
Thus a wire with a diameter of 25 mils has an area of 252 = 625 circular mils.
When using the English system, formula 3) becomes
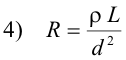
where:
ρ = the resistance, in ohms, of one mil-foot of wire i.e. the resistance in ohms of one foot of wire whose diameter is one mil
L = length of the wire in feet
d = diameter of the wire in mils
Problem. Find the resistance of 100 feet of No. 24 copper wire.
Solution. From a handbook (e.g. Eshbach. Handbook of Engineering Fundamentals) we find that No. 24 copper wire has a diameter of 0.0201 inches, or 20.1 mils, and a resistivity of ρ = 10.3 ohms/ mil-foot. Substituting these values into 4) gives
![]()
Temperature and resistivity. The resistivity of all conducting materials is affected by temperature. It is possible to represent the resistivity as a function of temperature by a mathematical series. If ρ0 is the resistivity of the material at some reference temperature t0, the resistivity ρt at temperature t can be expressed as
5)ρt = ρ0 [1 + α(Δt) + αʹ(Δt)2 + .... ]
Material |
Resistivity ρ in ohm-cm at 20oC |
Temperature Coefficient α per oC at 20o C |
Aluminum |
2.83×10-6 |
0.0039 |
Carbon |
3.5×10-3 |
-0.0005 |
Copper |
1.72×10-6 |
0.0038 |
Iron |
10×10-6 |
0.0050 |
Manganin |
44×10-6 |
0.00001 |
Nichrome |
100×10-6 |
0.0004 |
Platinum |
10×10-6 |
0.0038 |
Silver |
1.63×10-6 |
0.0038 |
Tungsten |
5.51×10-6 |
0.0045 |
Resistivity of conducting materials
Table 1
where α, αʹ, etc. are constant coefficients to be evaluated at the reference temperature t0,
Δt = t - t0
and temperatures are degrees Centigrade. Often the first two terms are adequate, giving
6) ρt = ρ0 [1 + α(Δt)]
where α is called the temperature coefficient of resistivity at the temperature t0.
Superconductivity. The resistivity of all metals approaches zero as the temperature approaches absolute zero. For some substances (e.g. lead, mercury, tin, aluminum, titanium) the resistivity drops completely to zero at some transition temperature above absolute zero. A current once started in a superconductor will continue indefinitely.
Def. Current density. The quantity of charge passing through a unit area perpendicular to the direction of motion of the charge, per unit time.
The current density is the electric current per unit area of cross section. It is a vector J pointed in the direction of the current I whose magnitude is given by I/A where A is the cross-sectional area of the current i.e.
7) J = I/A
where the current I is a vector.
Theorem. The resistivity is given by
8) ρ = E/J
where E is the magnitude of the electric field intensity and J is the magnitude of the current density.
Drift velocity. The drift velocity is given by
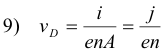
where
VD = drift velocity
i = current flow rate
A = cross-sectional area of the current
n = number of free electrons per unit volume
e = electron charge
j = current density
Problem. Estimate the drift velocity of the free electrons in a copper conductor of cross-sectional area 1 cm2 in which the current is 1 amp.
Solution. Using
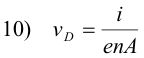
The value of e is approximately 1.6×10-19. Calculations have given the value of n for copper to be about 8.5×1028 free electrons per cubic meter, assuming that each copper atom contributes two free electrons. The area A is 10-4 m2 and the value of the current i is 1. Substituting these values into 7) gives
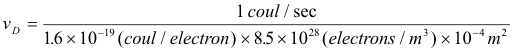
![]()
References
1. Dull, Metcalfe, Brooks. Modern Physics.
2. Sears, Zemansky. University Physics
3. Semat, Katz. Physics.
4. Freeman. Physics Made Simple.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life