Light. Law of reflection and refraction. Angle of incidence, reflection, refraction. Optical density. Index of refraction. Critical angle and total internal reflection. Phase changes on reflection.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Light. Laws of reflection and refraction. Angle of incidence, reflection, refraction. Optical density. Index of refraction. Critical angle and total internal reflection. Phase changes on reflection.

Reflection of light. Reflection is the turning back of light waves from a surface. Light is reflected from a surface in a way similar to the way an elastic ball rebounds from a wall or a sound wave is reflected from a cliff.

The amount of light an object reflects depends on:

1) The kind of material it is made of

2) The smoothness of the surface (how polished it is)

3) The angle at which the light strikes its surface

Polished aluminum is a better reflector than polished black plastic. Polished metal is a much better reflector than rough metal. The glare of the setting sun on the surface of a lake shows that light is strongly reflected when light rays strike a surface at an oblique angle.

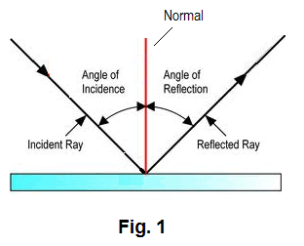
Def. Normal. A line drawn perpendicular to a plane.

Def. Angle of incidence. The angle between the incident ray and the normal drawn to the point of incidence. See. Fig. 1.

Def. Angle of reflection. The angle between the reflected ray and the normal drawn to the point of incidence. See Fig. 1.

Substance	Index of Refraction
Air	1.0003
Ice	1.31
Water	1.33
Gasoline	1.38
Ordinary glass	1.5
Plexiglas	1.51
Dense optical glass	1.6-1.9
Zircon	1.92
Diamond	2.42

Table 1

Def. Plane of incidence. That plane containing the incident ray and the normal at the point of incidence.

Experiment gives the following laws of reflection for light.

Laws of Reflection:

1. The angle of reflection is equal to the angle of incidence.

2. The reflected ray lies in the plane of incidence (it lies in the plane containing the incident ray and the normal at the point of incidence.)

These laws of reflection are also valid for the reflection of other types of waves, including sound waves.

Refraction of light.

Optical density. A measure of the speed at which light is transmitted through a transparent substance. The higher the optical density of the medium, the slower light travels in the medium.

Def. Index of refraction. The ratio of the speed of light in a vacuum to its speed in a given substance.

The index of refraction of a substance is a measure of its optical density. Table 1 contains the index of refraction of various substances.

In general, when a beam of light, traveling in a transparent medium, strikes the surface of a second transparent medium of a different optical density, the beam will split. Part of it will be reflected back into the original medium and the other part will pass on into the new medium as a refracted beam. Refraction is the bending of light rays as they pass from one medium into another medium of different optical density.

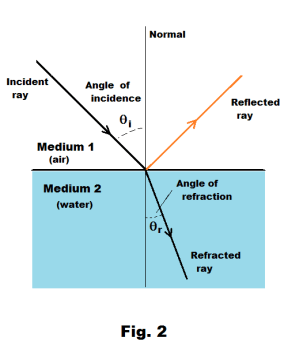
Def. Angle of refraction. The angle between the refracted ray and the normal drawn to the point of refraction. See Fig. 2.

Laws of refraction.

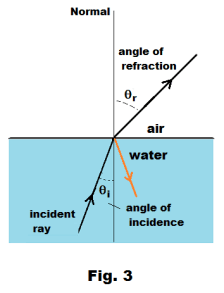
Law 1. When a ray of light passes obliquely from a medium of lesser to one of greater optical density, it is bent toward the normal. Conversely, a ray of light passing obliquely from a denser to a less dense medium is bent away from the normal. See Figures 2 and 3.

Law 2. The refracted ray lies in the same plane as the incident ray and the normal.

Law 3. The angle of incidence θ_i and the angle of refraction θ_r are related as follows:

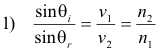
where

v₁ = velocity of light in Medium 1

v₂ = velocity of light in Medium 2

n₁ = index of refraction of Medium 1

n₂ = index of refraction of Medium 2

The constant

is called the coefficient of refraction of Medium 2 with respect to Medium 1. When Medium 1 is a vacuum, it is simply called the (absolute) index of refraction of Medium 2.

The index of refraction for air is essentially the same as that for a vacuum since the speed of light in air is essentially the same as in a vacuum.

Law 3 is known as Snell’s Law. We see from 1) that the connection between θ_i and θ_ris given by the simple relationship

2) n₁ sin θ_i = n₂ sin θ_r

Fig. 2 shows a ray passing from a less dense medium (air) into a more dense medium (water). Fig. 3 shows a ray of light passing from a denser medium (water) into a less dense medium (air). As can be seen, in the later case the ray is bent away from the normal.

When a ray of light passes from a medium of one optical density to one of a different density, why does it abruptly change direction? Insight can be seen in the following: Suppose you are driving down a highway and your right front wheel accidently goes off the hard pavement onto a soft shoulder. The right front wheel will be slowed down by the soft shoulder and the vehicle will be pulled to the right. It will cause the vehicle to veer to the right.

Derivation of formula sin θ_i /sin θ_r= v₁/v₂ . Consider Fig. 4 in which a plane wave is incident on the boundary between two media at an angle of incidence of θ_i. Assume the velocity of light in Medium 1 is v₁ and the velocity in Medium 2 is v₂. Suppose that at time t = t₀ the wave front is at position AB where it is just making contact with the boundary at point A. Suppose that at time t = t₀ + Δt wave front AB has advanced to the position CD where we use Huygens’ Principle for finding the new position of the wave front. Now AC is perpendicular to CD and AB is perpendicular to BD. In addition,

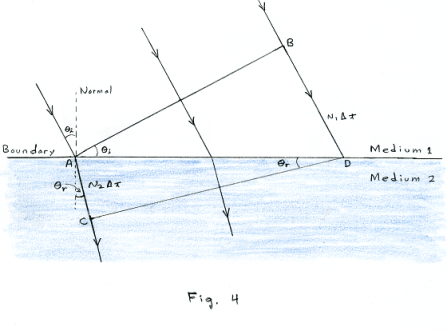
BD = v₁Δt

AC = v₂Δt

Hence

-----------------------------------

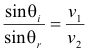
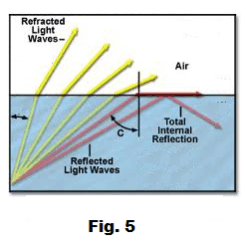
The critical angle and total internal reflection. In Fig. 3 is shown a ray of light passing from a medium of higher optical density into a medium of lower optical density (in this case from water into air). If we increase the angle of incidence θ_i, the angle of refraction θ_r will also increase. If we keep increasing the angle of incidence θ_i, we reach a point where the angle of refraction θ_r becomes 90^o. The value of the angle of incidence θ_i, at which the angle of refraction becomes 90^o is called the critical angle. What happens when we increase θ_i beyond the critical angle? We then have total internal reflection. Fig. 5 shows this situation. What actually happens is that when the angle of incidence θ_i is less than the critical angle, there is both a refracted beam and a reflected beam. As the angle of incidence increases, the strength of the reflected beam becomes stronger at the expense of the refracted beam. When the angle of incidence passes the critical angle, the refracted beam and the reflected beam become one, giving total reflection.

The critical angle for any two given substances can be found by setting θ_r = 90^o or sin θ_r =1 in Snell’s Law. Thus

sin θ_c = n₂/n₁

Example. Compute the critical angle of an air-glass surface, taking 1.50 as a typical index of refraction of glass.

sin θ_c= 1/1.50 = 0.67

Thus θ_r = 42^o.

Applications of total internal reflection. Applications of total internal reflection include:

1. Reflecting prisms as used in binoculars, reflecting telescopes, submarine periscopes, etc.

2. Cutting of gems, such as diamonds.

3. Rods of clear, colorless plastic that can be bent into unusual shapes, used for transmitting light. Beams of light entering one end of the rod are totally reflected by the walls and emerge at the other end.

Phase changes on reflection. For normal and nearly normal angles of incidence, light traveling in a rarer medium will undergo a 180^o phase change when reflecting from a denser medium. There is no phase change at other angles and no phase change when light traveling in a denser medium reflects at a rarer medium. When light passes from one medium to another, there is no phase change.

Change in wavelength when light passes from one medium into another. When light passes from one medium to another, not only does its speed change, but its wavelength also changes. Its frequency remains the same. The wavelength, frequency and speed are related by the formula v = fλ. If v₁, λ_1, n₁ are the speed, wavelength, and index of refraction in Medium 1 and v₂, λ₂, n₂ are the speed, wavelength, and index of refraction in Medium 2, then

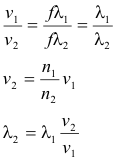
References

Dull, Metcalfe, Brooks. Modern Physics

Sears, Zemansky. University Physics

Freeman. Physics Made Simple