Mechanical equivalent of heat. Thermodynamics. Internal energy. PV diagram. Enthalpy. Molar heat capacity. Isobaric, isovolumic, isothermal, and adiabatic processes. Entropy, Free energy.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Mechanical equivalent of heat. Thermodynamics, Internal energy. PV diagram. Enthalpy. Molar heat capacity. Isobaric, isovolumic, isothermal, and adiabatic processes, Entropy, Free energy.

The nature of heat. For a number of years heat was viewed by most researchers as an invisible weightless fluid called caloric that was produced when a substance burned. It was viewed as a substance that was transmitted by conduction from one body to another. The theory was under attack by a few researchers in the first half of the 19^th century. Some of the basic assumptions of this view were questioned by Count Rumford around 1800 in his studies on heat done in connection with his work in the boring of cannon for the Barvarian government. He discovered, for example, that an unlimited amount of heat could be produced through friction by using a dull cutting instrument, thus bringing into question the idea that heat was a material substance. Humphry Davy and others followed Rumford in questioning the caloric theory. In 1842 J. R. Mayer proposed that heat was a form of energy, laying the foundation for the principle of the conservation of energy. Then in 1850 James Prescott Joule, after many experiments, published a work in which he showed that a definite amount of mechanical energy in the form of work could always be transformed into the same amount of heat. So around the middle of the 19^th century the caloric theory of heat gradually gave way to the present theory that heat is simply a form of energy, convertible into a specific amount of mechanical energy.

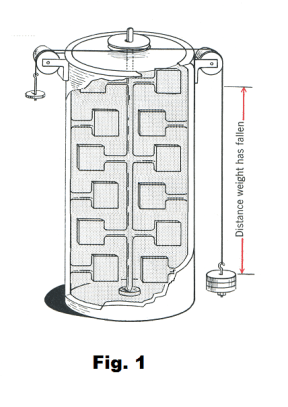
The mechanical equivalent of heat. A simplified version of the apparatus used by Joule in deriving the mechanical equivalent of heat is shown in Fig. 1. The weights are allowed to fall a certain distance and as they fall, the cord to which they are attached turns the shaft and paddles. The movement of the paddles warms the water by friction. All of the work done by the weights in moving through a specified distance is converted into heat. The amount of work done on the system is computed by multiplying the amount of weight by the distance moved. The amount of heat produced is computed by multiplying the mass of the water by the increase in temperature. Joule found that 772 ft-lb of work produced one Btu of heat. More recent experiments have given a figure of 778 ft-lb per Btu. In the metric system, one calorie equals 4.19 joules of work.

Thermodynamics. Thermodynamics is a study of the quantitative relationships between heat and other forms of energy. The history of thermodynamics traces back to the work of Sadi Carnot regarding the efficiency achievable with steam engines. Steam engines, gasoline engines and diesel engines all work on cycles that involve the heating of a working fluid in a cylinder fitted with a piston and the production of a power stroke that does work. Refrigeration devices such as refrigerators, air conditioners, heat pumps, etc. involve the compression and expansion of a working fluid (the refrigerant) and the absorption and removal of heat from the fluid. All of the above involve one or more of the following operations:

1) absorption of heat by the working fluid

2) removal of heat from the working fluid

3) expansion of the working fluid in the production of work

4) compression of the working fluid

Internal energy U. The internal energy U of a substance is the sum total of the kinetic and potential energies of its molecules. Not enough is currently known about molecular structure for us to ascertain the value of U for a substance. However, if we add a quantity of heat to a substance and no work has been done by the substance or on the substance, we can assume that the value of U for the substance has been increased by the amount ΔU equal to the amount of heat added.

The first law of thermodynamics states that energy can neither be created nor destroyed. A corollary is the following:

The increase in internal energy ΔU of a substance is equal to the heat Q added to the substance minus the work W done by the substance i.e.

ΔU = Q - W

If the substance absorbs heat from the surroundings, Q is positive. If it gives up heat to the surroundings, Q is negative. If work is done by the substance against the surroundings, W is positive. If work is done by the surroundings against the substance, W is negative.

Consider a cylinder of cross-sectional area A fitted with a frictionless and weightless piston. A gas contained within the cylinder is heated and is allowed to expand against an opposing pressure p (where the pressure p may, for example, be the pressure exerted by the atmosphere). See Fig. 2.

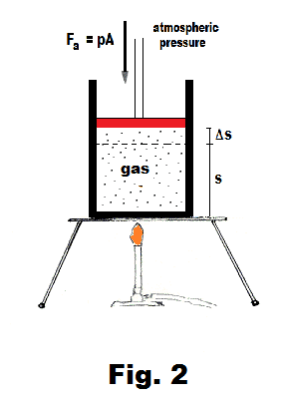
In many processes in nature, gases expand against the atmosphere. Most chemical reactions in which gases are produced are of this type. To better understand the thermodynamic aspects of these processes it is useful to consider as a model, a cylinder fitted with a frictionless and weightless piston and filled with gas as shown in Fig. 2. Let us heat the air. As it is heated it expands, pushing the piston out against the atmosphere and in so doing, it does work, losing some of its energy to the work done. We are in this way led to the general problem of a gas expanding against a constant pressure (where that constant pressure is the pressure of the atmosphere).

In Fig. 2, the force exerted by the piston on the gas is given by F_a = pA where p is the atmospheric pressure and A is the cross-sectional area of the cylinder. The force exerted by the gas on the piston is a vector F_g of the same magnitude as F_a, but opposite in direction. If the gas expands from a volume V₁ to a volumeV₂, the work W done by the gas on the atmosphere is given by F_g times the distance through which it acts, Δs:

W = F_g∙Δs = pA∙Δs = pΔV

where ΔV is the increase in volume V₂ - V₁.

If a quantity of gas is heated in a closed container its temperature will increase and its pressure will increase in proportion to its temperature increase. Its internal energy will increase by the amount of heat added to it. If a quantity of gas is heated in a cylinder fitted with a weightless piston and the air is allowed to expand against the piston, the piston exerting a constant force against it corresponding to the pressure of the atmosphere, then work is done against the atmosphere. The internal energy of the gas will increase by the quantity

of heat added minus the amount of work done against the atmosphere.

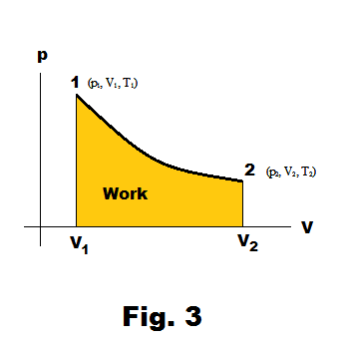
Work done in expansion. If a working fluid expands from an initial volume V₁ to a final volume V₂ in going from an initial point 1 (p₁, V₁, T₁) to final point 2 (p₂, V₂, T₂), the amount of work done is given by

where p is a function of V. See Fig. 3.

PV (pressure-volume) diagram. When a working fluid expands in a cylinder, doing work against its surroundings, the working fluid goes through a succession of PVT states. These states correspond to some path connecting an initial point 1 (p₁, V₁, T₁) to a terminal point 2 (p₂, V₂, T₂) on the PVT surface of the fluid. See Fig. 5.

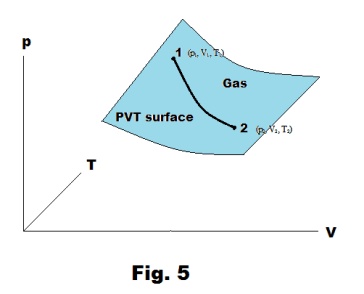
A PV diagram is a plot of pressure versus volume along some path between some beginning point 1 (p₁, V₁, T₁) and terminal point 2 (p₂, V₂, T₂) on the PVT surface. In general, the temperature will vary continuously from point to point along the path. See Fig. 3.

Work done in compression. Work done in expansion is positive and work done in compression is negative. Suppose we compute the work done by compression in going from point 2 to point 1 in Fig. 3 using the path shown. Then the amount of work done would be the same as that done in expansion but negative in sign. In expansion, work is done by the fluid against the surroundings. In compression, work is done by the surroundings against the working fluid.

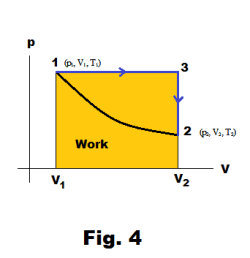
The amount of work done depends on the path. In examining Fig. 3 it is obvious that if a different path is taken in going from point 1 to point 2, a different amount of work will be done. Consider the path from 1 → 3 → 2 shown in Fig. 4. This would correspond to keeping the pressure constant from 1 to 3 (an isobaric process) and then keeping the volume constant from 3 to 2 (an isovolumic process). The work would then be that of the area under the line 1→3 as shown.

__________________________________________________________________________

Definitions

Def. Medium (or working fluid, or working substance ). The material substance which absorbs, rejects, or transports energy during a thermodynamic process or cycle.

Examples: 1) water and its vapor in a steam power plant. 2) the refrigerant in a refrigerator.

Physical properties of a medium. The pressure, temperature, specific volume, etc. of the medium which define its PVT (pressure, volume, temperature) state. Sometimes called the defining coordinates of the medium.

Def. Specific volume. The volume of a unit mass of a medium.

Def. Temperature, T. An index or measure of the molecular activity of matter.

Def. State of a medium (or working substance). The PVT (pressure, volume, temperature) state of the medium. Different states of a medium correspond to different defining coordinates (p, V, T) and different points on its PVT surface. Different points on the PVT surface of the substance correspond to different states.

Def. Process. An operation that produces a change of state of a system. Example: Heating the gas shown in Fig. 2 above and letting it expand against the atmosphere from volume V₁ to volume V₂ is a process. The process has changed the state of the gas, taking it from a State 1 (p₁, V₁, T₁) to a State 2 (p₂, V₂, T₂). The process involves progressing through a succession of PVT states which correspond to some path on the PVT surface of the gas.

Def. Cyclic process. A process in which the final and initial states of the system are identical.

Def. Thermodynamic system. The region enclosing the matter involved in the energy transformation being studied.

Def. Surroundings. The region outside the thermodynamic system, separated from it by an imaginary or real line or envelope called the boundary.

Def. Open and closed systems. A system is called closed if no mass crosses the boundary. It is called open if there is a mass exchange between the system and the surroundings.

The solution of many thermodynamic problems dictates the limitation of the system to the working fluid or medium. Other problems dictate the inclusion in the system of various pieces of equipment with the working fluid.

__________________________________________________________________________

Changes in internal energy U. ΔU depends only on the initial and final states of the system and is independent of the particular path linking the initial and final points i.e.

ΔU = U₂ - U₁

in which

ΔU = change in internal energy

U₂ = internal energy of system in the final state

U₁ = internal energy of system in the initial state

● The amounts of heat absorbed and work done depend on the process and thus depend on the path taken and are called path functions.

Internal energy of an ideal gas. The internal energy of one mole of an ideal gas is given by

where N₀ is the number of molecules in a mole of the gas (Avogadro’s number), m is the mass of a molecule, the kinetic energy of a single molecule is ½ mv², and the over-bar indicates an average. The assumptions of the kinetic theory of gases lead to the following relationship between the internal energy U of a mole of an ideal gas and the pressure and volume:

The perfect gas law states that for one mole of an ideal gas

3] pV = RT

From 2] and 3] we get

Thus the internal energy of an ideal gas is proportional to the Kelvin temperature.

Def. Heat content (or enthalpy), H. The quantity H = U + pV is called the heat content or enthalpy.

In a constant-pressure process

ΔU = Q - W = Q - pΔV

where Q is the heat added and W is the work done.

Thus

Q = ΔU + pΔV = U₂ - U₁ + (pV₂ - pV₁) = (U₂ + pV₂) - (U₁ + pV₁) = H₂ - H₁ = ΔH

We have thus shown that the heat absorbed in a constant-pressure process is equal to the increase in heat content or enthalpy. ΔH like ΔU depends only on the initial and final states of the system.

Def. Molar heat capacity. The number of calories needed to raise the temperature of one mole of a substance one degree centigrade.

Def. Molar heat capacity of a gas maintained at constant volume, C_V. The number of calories needed to raise the temperature of one mole of a gas one degree centigrade when the volume is kept constant.

Def. Molar heat capacity of a gas at constant pressure, C_P. The number of calories needed to raise the temperature of one mole of a gas one degree centigrade when the pressure is kept constant.

Relationship between C_V and C_P for an ideal gas. For an ideal gas

1) C_P - C_V = R

where R is the universal gas constant. If C_P and C_V are in cal/mole∙C^o, then R = 1.99 cal/mole∙C^o and, in this case, C_P = C_V + 2.

_______________________________________________________________________

Derivation.

C_P - C_V = W = pΔV = p(V₂ - V₁) = R(T₂ - T₁)

Since T₂ - T₁ = 1, we have

C_P - C_V = R

_______________________________________________________________________

The value of C_Vfor an ideal monatomic gas. For an ideal monatomic gas

Proof

From 1) and 2) we get

The ratio C_P/C_V is denoted by γ. Thus for an ideal monatomic gas

4) γ = 5/3 = 1.67

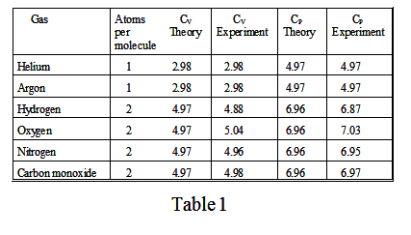
For monatomic and diatomic molecules the agreement between theory and experiment is quite good. See Table 1.

First law of thermodynamics. Let a quantity of heat Q be added to a system that also does external work W. Then the change in internal energy ΔU of the system is given by

ΔU = Q - W

If Q is greater than W, the internal energy of the system increases by the amount Q - W. If Q is less than W, the internal energy decreases.

Specific heat of a gas. The specific heat of a gas at constant volume, c_v,, is the amount of heat needed to raise a unit mass of the gas one degree when volume is kept constant. The specific heat of a gas at constant pressure, c_p, is the amount of heat needed to raise a unit mass of the gas one degree when pressure is kept constant.

Constant-pressure (isobaric) processes. A mass m of gas is heated at a constant pressure p from a temperature T₁ to a temperature T_2. Then:

Amount of heat Q added: Q = mc_pΔT

Increase in internal energy ΔU: ΔU = mc_vΔT

Work done: W = Q - ΔU = m(c_p - c_v)ΔT = pΔV

where c_v is the specific heat of the gas at constant volume, c_p is the specific heat of the gas at constant pressure, and ΔT = T₁ - T₂.

Constant-volume (isovolumic) processes. A mass m of gas is heated at a constant volume from a temperature T₁ to a temperature T₂. Then:

Amount of heat Q added: Q = mc_vΔT

Increase in internal energy ΔU: ΔU = Q = mc_vΔT

Work done: W = 0

where c_v is the specific heat of the gas at constant volume, c_p is the specific heat of the gas at constant pressure, and ΔT = T₁ - T₂.

Constant-temperature (isothermal) processes. When a mass m of gas expands isothermally against a pressure from an initial volume-pressure (V₁, p₁) to a final volume-pressure (V₂, p₂), the change in internal energy is zero and the heat added equals the external work done by the gas (Q = W).

Amount of heat Q added:

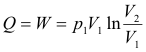
Increase in internal energy ΔU: ΔU = 0

Work done:

Proof

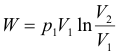
Adiabatic process. An adiabatic process is one in which no heat enters or leaves the system. Thus in an adiabatic process ΔQ = 0. Many of the processes of nature and engineering are adiabatic or nearly so. A process may be nearly adiabatic if it takes place inside a chamber with highly insulated walls or if it is performed so quickly that there is little time for heat to transfer. The compression of the mixture of gasoline vapor and air during the compression stroke of a gasoline engine is an example of an approximately adiabatic process. The expansion of the combustion products during the power stroke is also approximately adiabatic.

In an adiabatic process Q = 0 = ΔU + W, so ΔU = - W. This means that the increase in internal energy is equal to the external work done on the system, (or that the decrease in internal energy is equal to the external work done by the system). In an adiabatic process,

where γ = C_p / C_v= c_p / c_{v .}

Proof

Problem. The compression ratio of a diesel engine, V₁ /V₂, is about 15. Assume that at the start of the compression stroke the cylinder contains air at 15 lb/in² and 60^o F. Compute the pressure and temperature at the end of the stroke. The value of γ for air is 1.40. Assume that air behaves like an ideal gas and that the compression is adiabatic.

Solution. Since p₁V₁^γ = p₂V₂^γ, we have

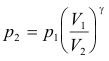
log p₂ = log p₁ + γ log (V₁ / V₂)

= log 15 + 1.4 log 15

= 1.176 + 1.646 = 2.822

p₂ = 663 lb/in²

To find the temperature at the end of the stroke we can use the ideal gas law, pV = nRT. We note that 60^o F = 520^o R.

Now P₁V₁ = nRT₁ and P₂V₂ = nRT₂ . Dividing the second by the first we obtain

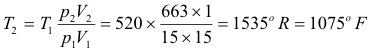
Second law of thermodynamics. The second law of thermodynamics has been stated in a number of ways. Some common statements are:

1. Clausius: It is impossible to construct a machine that, while operating in a cycle, will produce no other effect than the transfer of heat from a cold body to a body of higher temperature.

2. Kelvin-Planck: It is impossible to construct an engine that, while operating in a cycle, will absorb heat from a single reservoir and produce an equivalent amount of heat.

Mechanical energy can be converted completely into heat, but heat cannot be converted completely into mechanical energy. This is an example of a one-sidedness of nature that is revealed in many ways. Heat always flows from a hotter to a cooler body and never the other way; rocks weather, iron rusts, people grow old. These are all examples of irreversible processes that take place in one direction only and express the second law of thermodynamics.

Entropy. A thermodynamic quantity representing the unavailability of a system's thermal energy for conversion into mechanical work. It is often interpreted as the degree of disorder or randomness in the system.

The concept of entropy is closely associated with the Second Law of Thermodynamics and the concepts of spontaneous and nonspontaneous processes. Many processes in nature occur spontaneously when left to themselves: water runs downhill; heat flows from hot bodies to cooler bodies; chemical reactions proceed to equilibrium; gases expand from regions of high pressure to regions of low pressure. For any spontaneous process it is possible to devise, in principal at least, a mechanism for getting useful work from the process. For example, falling water can turn a water wheel, an expanding gas can push a piston, etc. It is obvious that as a spontaneous process occurs a system loses ability to do useful work.

The term nonspontaneous is applied to the reverse of a spontaneous process, e.g., water flowing uphill. Nonspontaneous processes can only be made to occur by supplying energy from outside the system. For example, energy must be supplied to pump water uphill or to compress a gas. Since the energy required must be supplied by a spontaneous process, it is obvious that a spontaneous process can be reversed only by harnessing energy from another spontaneous process.

When a spontaneous process occurs by itself no useful work is done, e.g., as when a gas expands into a vacuum. The maximum amount of work is obtained from a spontaneous process when it is carried out reversibly, that is, in such a way that at any time it can be reversed by an infinitesimal change.

Daniels, Alberty. Physical Chemistry

Def. Entropy. In thermodynamics, a property of a system which remains constant during a reversible adiabatic process, and which is defined by the equation

dS = dQ/T

where dS is an infinitesimal change in the entropy of a system, dQ is the infinitesimal quantity of heat that enters the system, and T is the Kelvin temperature of the system.

In statistical mechanics, entropy is a quantity proportional to the logarithm of the probability of the state considered, which is defined by the equation

S = k log_e P + constant

where S is the entropy, k is the Boltzman constant, and P is the statistical probability. It can be shown that the two definitions are equivalent.

The International Dictionary of Applied Mathematics

Def. Statistical Mechanics. That part of physics where one derives the properties of matter in bulk from a knowledge of its constituent parts. It is developed from kinetic theory but is distinguished from it by considering ensembles of systems rather than single systems.

The International Dictionary of Applied Mathematics

Third Law of Thermodynamics. The entropy of a perfect crystalline substance (which is most crystals) at 0^o K is zero.

The absolute entropy of a perfect crystalline substance at constant pressure and a temperature T is given by

To evaluate the absolute entropy we make a plot of C_p versus log T. A typical plot for a solid is shown in Fig. 6. The area under the curve from T = 0 to T = T is determined by some means (as by a planimeter) and multiplied by 2.303.

Experimental measurements of C_P can be made down to temperatures as low as 10 to 15 degrees K. Below this temperature extrapolation to 0^o k can be made with various semiemperical equations. If a transition, such as fusion, vaporization, or sublimation, occurs, there will be a discontinuity in the C_p versus log T curve. In this case a ΔS = q_rev /T term will have to be added to ΔS as calculated from the graphical integration for each discontinuity.

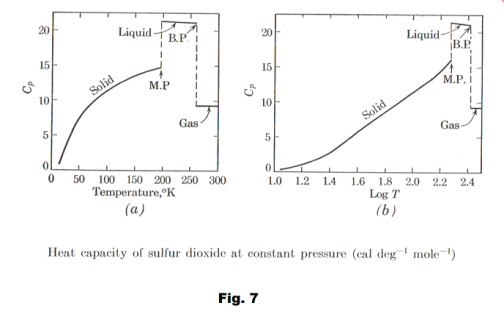
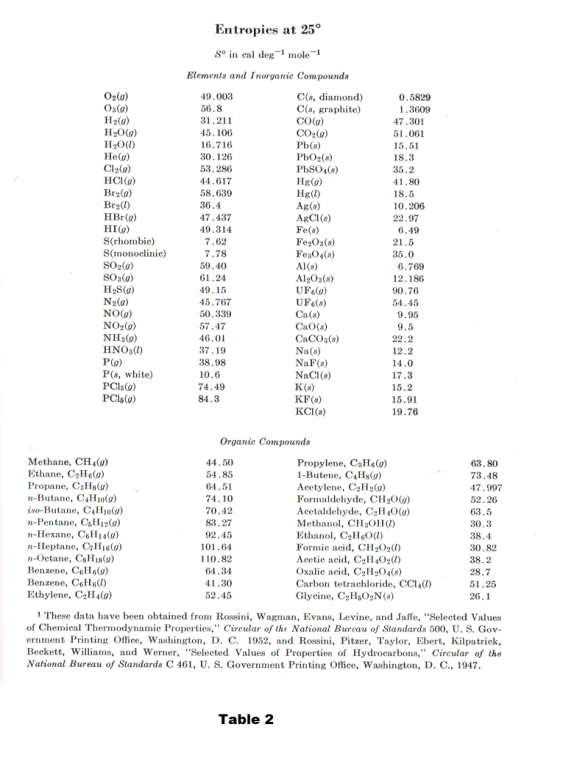
Heat capacities for SO₂ as a function of T and log T are shown in Fig. 7. Table 2 gives the entropies at 1 atm pressure and 25^o C for a number of elements and compounds.

Physical interpretation of Entropy. Entropy can be viewed as a measure of the disorder of a system. A pure crystalline substance at 0^o K consists of stationary ions, atoms, or molecules perfectly arranged in a crystal lattice, motionless, with an entropy of 0. As the temperature rises, the units in the lattice absorb heat resulting in various vibrational, rotational, and translation motions; their energy increases and their entropy increases. On further heating the solid finally melts, most of the order is destroyed, and the entropy increases further. More heating results in vaporization and a further increase of disorder and increase in entropy.

Free Energy, F. Free Energy, F is defined as

F = H - TS

where

H = Enthalpy (or Heat content) = U + pV,

T = absolute temperature

S = Entropy

and represents that portion of heat content which is isothermally available.

Work Content, A. Work Content, A is defined as

A = U - TS

and represents that portion of the internal energy U which is isothermally available.

Like internal energy, F and A depend only on the initial and final states of the system.

References

Dull, Metcalfe, Brooks. Modern Physics.

Sears, Zemansky. University Physics.

Schaum. College Physics.

Semat, Katz. Physics.

Daniels, Alberty. Physical Chemistry.

Kittsley. Physical Chemistry.

Warner. Thermodynamic Fundamentals.

Zemansky. Heat and Thermodynamics.