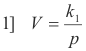
Website owner:  James Miller

Proof. Given Vp = k₁ at constant temperature and V = k₂T at constant pressure, we wish to prove that Vp = kT.

Because Boyle’s law is applicable only at constant temperature and the Charles-Gay-Lussac is only applicable at constant pressure, it is not immediately clear that simple combination of the two laws is justified. However, Boyle’s law can be written as

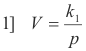
and so it is clear that the volume is a function of the pressure and the absolute temperature i.e.

2]        V = f(p, T)

By partial differentiation we obtain

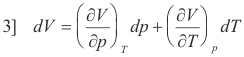
Taking the derivative of 1] with respect to p we get

Taking the derivative of V = k₂T with respect to T

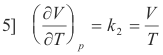
Substituting 4] and 5] into 3] we obtain

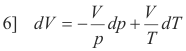
or

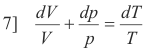
Integrating

8]        ln V + ln p = ln T + ln k (a constant)

Taking antilogarithms we get

9]        pV = kT