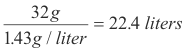
Website owner: James Miller
Standard Temperature and Pressure. Gram-molecular weight. Mole. Avogadro’s Law. Boyle’s law. Charles-Gay-Lussac’s law. Kelvin, Rankine temperature scale. Perfect-gas law. Kinetic Theory of Gases. Vapor pressure. Partial pressure. Dalton’s Law of partial pressures. Absolute and relative humidity. Dew point.
Def. Standard pressure. The pressure exerted by a column of mercury exactly 760 mm high. This is approximately the average pressure at sea level and is called one atmosphere.
Def. Standard conditions. Standard Temperature and Pressure (STP). A temperature of 0oC (273oK) and a pressure of 760 mm of mercury (1 atmosphere).
Def. Molecular weight. The molecular weight of a compound is the sum of the atomic weights of all the individual atoms in the molecule as represented by its formula.
Example. Compute the molecular weight of H2SO4.
2 H = 2 × 1.008 = 2.016
1 S = 1 × 32.064 = 32.064
4 O = 4 × 15.994 = 63.998
Molecular weight = 2.016 + 32.064 + 63.998 = 98.078
Def. Gram-molecular weight. The number of grams of any compound that is exactly equal to its molecular weight.
Example. The gram-molecular weight of H2SO4 is 98.078 g since it has a molecular weight of 98.078.
Def. Gram-atomic weight. The number of grams of any element that is exactly equal to its atomic weight.
Syn. Gram-atom
Example. The gram-atomic weight of carbon-12 is 12 g since it has an atomic weight of 12.
Avogadro’s number. The number of atoms in a gram-atomic weight of any element is 6.023 ×1023 atoms. This number is known as Avogadro’s number. Moreover, the number of molecules in a gram-molecular weight of any compound is 6.023 ×1023 molecules (Avogadro’s number). [Why? Consider the following relationships: Let
wp = weight, in grams, of a proton (or neutron)
NA = Avogadro’s number (6.023 ×1023 )
wa = atomic weight of some element (= number of protons + neutrons in atom)
wga = gram-atomic weight of the element
Then these variables are related by
wga = NA×wa×wp
Let
wm = molecular weight of some compound (= number of protons + neutrons in molecule)
wgm = gram-molecular weight of the compound
Then
wgm = NA×wm×wp ]
Def. Mole. The amount of a substance containing the same number of basic units (atoms, molecules, ions, etc.) as there are atoms in 12g of carbon-12. This number is Avogadro’s number.
A mole of any compound is thus equal to its gram-molecular weight. A mole of any element is equal to its gram-atomic weight.
One mole of any substance contains the same number of molecules as a mole of any other substance. A mole of O2 contains the same number of molecules as a mole of CO2 or a mole of H2SO4. The number of molecules contained in a mole of any substance is given by Avogadro’s number, which is 6.023 ×1023 molecules.
Avogadro’s Law. At the same temperature and under the same pressure, equal volumes of gases contain the same number of molecules.
Q. How much space is occupied by a mole of oxygen, O2, at STP?
A. One liter of oxygen at STP weighs 1.43 g and a mole of oxygen weighs 32 g. The amount of space occupied by a mole of oxygen is then given by
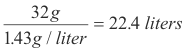
By Avogadro’s Law 22.4 liters of any other gas at STP will contain the same number of molecules as a mole of oxygen. Thus 22.4 liters of any gas at STP contains exactly one mole of the gas. Consequently if we know the weight of a gas we can compute its gram-molecular weight.
Def. Gram-molecular volume. The volume occupied by one gram-molecular weight (i.e. one mole) of a substance at STP. For all gases the gram-molecular volume is 22.4 liters.
Syn. molar volume, normal molar volume.
Formula weight. Many crystalline substances such as sodium chloride, NaCl, and hydrated cupric sulfate, CuSO4 ∙ 5 H2O, exist as ions and not in the form of molecules. In such substances the term molecular weight is incorrect and we use the term formula weight for the sum of the atomic weights of the atoms in the formulas.
Boyle’s law. If the temperature remains constant, the volume V of a given mass of gas varies inversely with the pressure p exerted on it. Stated mathematically
1) pV = constant (assuming constant temperature)
Thus if you double the pressure on a given volume of gas (and keep the temperature constant), the volume decreases to one half; if you triple the pressure the volume decreases to one third, etc.
We now consider Gay-Lussac’s law. It tells us how the volume of a gas varies with temperature if the pressure is kept constant. Experimentation led Gay-Lussac to the following law:
Gay-Lussac’s law. Let V0 be the volume of a given mass of gas at some reference temperature t0. Then if the pressure is kept constant, the volume V of the gas at temperature t is given by
2) V = V0[1 + β(t - t0)]
The numerical value of the coefficient β depends on the size of the degree (i.e. whether fahrenheit or centigrade) and on the reference temperature t0.
If, as is usually the case, the reference temperature is taken as 0o C, equation 2) becomes
3) V = V0C(1 + β0C t)
where V0C and β0C are the volume and coefficient corresponding to the reference temperature 0o C.
It is noteworthy that β0C has very nearly the same value for all gases. The value varies slightly from one gas to another, but the same value is approached by all gases at very low pressures. Determination of β0C for a number of gases at increasingly low pressures allows an extrapolation to zero pressure. This extrapolation gives the value
β0C = 1/273.16 per centigrade degree
for all gases. Consequently we can say:
The volume of a fixed mass of any gas kept at constant pressure increases by 1/ 273 of its value at 0o C for each centigrade degree increase in temperature.
Kelvin temperature scale. Thus from 3) we have
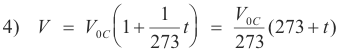
This equation suggests a new temperature scale in which the size of the degree is the same as in the centigrade scale but whose zero point is -273oC. This scale is called the Kelvin scale or absolute thermodynamic scale.
Kelvin temperature = 273 + centigrade temperature
Examples. 0oC = 273oK, 30oC = 303oK
The temperature -273oC is called the absolute zero of temperature.
Charles-Gay-Lussac Law. If the pressure is kept constant, the volume and temperature of a gas are related by
5) V = kT (assuming constant pressure)
where V is the volume, T is the Kelvin temperature, and k is a constant.
Ideal (or perfect) gases. Real gases obey Boyle’s law and the Charles-Gay-Lussac law quite closely at low pressures (less than about 2 atm) and more and more closely as pressures become lower. We call a gas that obeys the Boyle’s and Charles-Gay-Lussac laws exactly an ideal or perfect gas.
Rankine or fahrenheit absolute scale. In the Rankine scale the size of the degree is the same as the Fahrenheit degree but the zero point corresponds to 0oK or -273.16 oC. Because -273.6 oC corresponds to -460o F, the Rankine zero point corresponds to -460oF. Thus
Rankine temperature = 460 + Fahrenheit temperature
Examples. 0oF = 460oR, 32oF = 492oR
Theorem 1. The volume, pressure and temperature of a ideal gas are related by
6) pV = kT
where V is the volume of a given mass of gas, p is the pressure, T is the Kelvin temperature, and k is a constant.
Special case of one mole of gas. For the special case when the amount of gas is equal to one mole (one gram-molecular weight) equation 6) has the form
7) pV = RT
where R is called the molar gas constant.
Perfect-gas law. For the case of n moles of gas 6) has the form
8) pV = nRT
This is called the Perfect-gas law. It is also referred to as the equation of state for an ideal gas.
Evaluation of the molar constant R. R can be evaluated from the known fact that one mole of any gas at standard conditions (i.e. a pressure of 1 atm and a temperature of 0oC) occupies a volume of 22.414 liters. Thus:
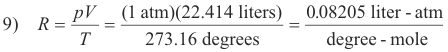
This value of R can be used if the pressure is expressed in atmospheres and the volume is expressed in liters. If other units are used for pressure and volume, R will have other values.
___________________________________________________________________
Kinetic Theory of Gases
Postulates for an ideal gas. The following idealized postulates are made for a gas:
1. A gas is composed of minute particles called molecules. For any particular gas, all molecules have the same mass and size.
2. The molecules of a gas are in a state of ceaseless, chaotic motion, during which they collide with each other and with the sides of the container.
3. The phenomenon called pressure is caused by collisions of the molecules with the sides of the container.
4. Collisions between molecules (and between molecules and the sides of the container) must be perfectly elastic (i.e. no kinetic energy is lost due to friction) since the pressure does not decrease with time.
5. At low pressures the molecules are so far apart that the intermolecular attractive forces (which decrease as the distances between the molecules increase) may be considered negligible.
6. At low pressures the volume occupied by the molecules may be considered negligible compared with the size of the container.
7. The absolute temperature of a gas is a function only of the average kinetic energy of all the molecules.
Source: Kittsley. Physical Chemistry. (COS) p. 12 - 15
A gas that satisfies the above postulates is called an ideal gas.
Relation between the kinetic energy of the molecules of an ideal gas and the pressure exerted on the sides of a container. We shall now derive the expression for the relationship between the kinetic energy of the molecules of an ideal gas and the pressure exerted on the sides of a container from considerations of a very simple case.
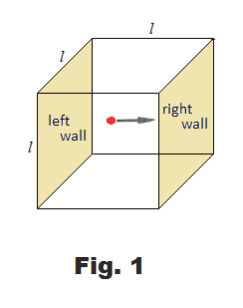
Consider a cubical box with edges of length l containing a single molecule of a gas. Assume the molecule has mass m and that it is moving toward the right wall of the cube with velocity of v1. See Fig. 1. Its momentum is then mv1. It now strikes the wall and rebounds. Since it is now moving in the opposite direction, its velocity is now -v1 and its momentum is -mv1. Thus the change in momentum per collision is mv1 - (-mv1) = 2mv1.
The molecule must travel to the left wall and back again before it can collide with the right wall again. Thus it must travel a distance of 2l between collisions with the right wall. If its velocity is v1, it follows that the number of collisions with the right wall per second is v1/2l, and the change in momentum per molecule per second at the right wall is
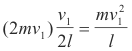
Now consider the cube to be filled with n molecules. These molecules are moving randomly in all directions, but it is possible to regard them as divided into three equal sets: one set moves right and left, another set moves up and down and the third set moves in and out (front to rear and back). Thus, of all the molecules in the cube, n/3 molecules may be considered moving perpendicular to the right wall of the cube.
Let v be the root-mean-square velocity of the n molecules as defined by
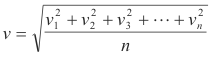
where:
v1 = velocity of molecule #1
v2 = velocity of molecule #2
............
vn = velocity of molecule #n
The average change in momentum per n/3 molecules per second at the right wall is then
![]()
According to Newton’s second law, the rate of change of momentum is equal to the force acting [F = ma so F = m dv/dt = d(mv)/dt ]. Hence, the force acting on the right wall of the cube is
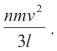
However, since pressure is force per unit area and since the area of a wall of the cube is l2 we have:
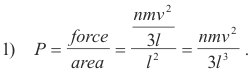
The volume of the cube is given by V = l3 and so 1) becomes
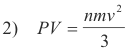
Since the pressure on all walls of the cube is the same, equation 2) is general. Equation 2) is called the fundamental kinetic equation.
Deduction of Boyle’s Law from the Fundamental Kinetic Equation. Multiplying numerator and denominator of the fundamental kinetic equation 2) by 2, we obtain
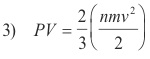
Since the kinetic energy of a moving molecule is equal to ½ mv2, the quantity in parentheses represents the kinetic energy of all the molecules. Furthermore, if temperature remains constant, the kinetic energy of the molecules remains constant. Thus
PV = ⅔(kinetic energy) = ⅔(constant) = a constant
which is Boyle’s law.
Avogadro’s Hypothesis. Equal volumes of gases under the same conditions of temperature and pressure contain the same number of molecules.
Deduction of Avogadro’s hypothesis. Given: Equal volumes V1 and V2 of two gases, Gas 1 and Gas 2, under equal pressures P1 and P2, respectively. Then P1V1 = P2V2 and from the fundamental kinetic equation 2) we have
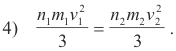
Since the temperature is constant, the average kinetic energies per molecule must be equal so
![]()
Dividing 4) by 5) we get
![]()
which is a mathematical statement of Avogadro’s hypothesis.

___________________________________________________________________
Behavior of real gases. Various equations have been devised for representing the behavior of real gases. For accurate work over a wide range of conditions a large number of constants are required. An equation which gives the relation between pressure, volume and temperature for a substance is called an equation of state. Van der Waals equation represents an early attempt to describe the behavior a real gas. It is
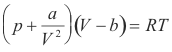
where a and b are constants that depend on the gas. The equation assumes one mole of gas. It is quite accurate for pressures of up to a few atmospheres but inadequate for high pressures.
Vapor pressure. When a volatile liquid is placed in a vacuum it will vaporize into a gas,

filling the space completely. Consider the following experiment. Place two simple barometer tubes close together as shown in Fig. 2 and introduce a drop or two of water into one of the tubes. The mercury in that tube will fall as soon as the water reaches the vacuum. This is because the water is converted into vapor which pushes the mercury downward. The pressure which the vapor exerts depends on the temperature, and for any given temperature the vapor pressure may be determined by measuring the difference in the height of the mercury in the two tubes. Vapor pressures of water are given in Fig. 3.
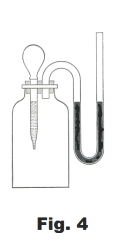
Water vapor exerts a pressure not only when it is introduced into a vacuum, but also if it is added to a dry gas. Dry gas in a dry bottle (Fig. 4) will show a marked increase in volume when a few drops of water are added. This is because the water evaporates and as a consequence the pressure of the water vapor is added to the pressure previously exerted by the dry gas. It can be shown that for any temperature the increase in pressure is exactly equal to the vapor pressure of water at that temperature. It is thus apparent that the evaporation of the water takes place to the same extent whether it is introduced into a dry gas or into a vacuum.
The molecules of a liquid, in their constant vibration, occasionally leave the surface of the liquid and dart off to become gas molecules. This phenomenon in which they escape from the liquid surface, dart off as gas molecules, is called evaporation. Their tendency to do this increases with increased temperature. This is because increased temperature implies increased internal energy and more vigorous molecular vibrations. If the vapor over a liquid is confined, it develops a pressure called vapor pressure which increases up to a value referred to as the saturated vapor pressure, at which an equilibrium is established.
Let us place a bell jar over a container of water as shown in Fig. 5. Initially the pressure inside
and outside the jar is the same. However, as the water evaporates, water molecules add to the
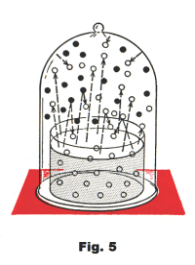
oxygen and nitrogen molecules of the air and there is an increased population of molecules inside the jar. This increased population is hitting the inside walls of the bell jar causing the pressure inside the jar to increase. As the interior of the jar becomes more and more thickly populated, more and more water molecules are being bounced back to the water surface to again become water molecules. Eventually a point is reached in which the number of molecules returning to the surface is equal to the number leaving it. At this point the number of water vapor molecules inside the jar becomes constant. These water vapor molecules exert a pressure on the walls of the bell jar in addition to the pressure being exerted on it by the air molecules. This added pressure from the water vapor molecules is called the saturated vapor pressure of the water vapor.
The saturated vapor pressure of a liquid is conventionally simply called the vapor pressure as revealed in the following definition:
Def. Vapor pressure. The pressure exerted by a vapor in equilibrium with the solid or liquid phase of the same substance.
Connection between vapor pressure and the boiling point of a liquid. The vapor pressure of water at a temperature of 100o C is 760 mm of mercury, or one atmosphere. This is the normal boiling point of water. When we heat a liquid its vapor pressure increases. When the vapor pressure of the liquid reaches the pressure of the air above it, it boils (where boiling is simply very rapid vaporization). If we reduce the air pressure above water to 528.8 mm of mercury, the water will boil at 90o C since 528.8 mm of mercury is the vapor pressure of water at 90o C. If we increase the air pressure above water to 1490 mm of mercury, the water will boil at 120o C. This is what is done with a pressure cooker. At such temperatures food will cook in one-half to one-third the time needed at 100o C.
See Vapor Pressure
Def. Partial pressure. In a mixture of gases, each gas has a partial pressure which is the hypothetical pressure of that gas if it alone occupied the volume of the mixture at the same temperature. The total pressure of an ideal gas mixture is the sum of the partial pressures of each individual gas in the mixture. (Wikipedia)
Dalton’s law of partial pressures. The total pressure of a gaseous mixture is equal to the sum of the partial pressures of the gases of which it is composed. The partial pressure of a component gas in a gaseous mixture is the pressure which the component would exert if it alone occupied the entire space.
Dalton’s law of partial pressures follows directly from the assumptions for an ideal gas. If we have n different gases enclosed in a cubical container, the total force that the n gases exert against the wall of the container will be given by the sum of forces that the individual gases exert on the wall of the container.
Dalton’s law is strictly valid only for ideal gases. At pressures up to few atmospheres gas mixtures can be regarded as ideal gases and this law can be applied.
Humidity. There is always some water vapor in the air. The amount may vary from place to place. In a particular location the amount will depend on temperature, wind, rainfall, and other weather conditions.
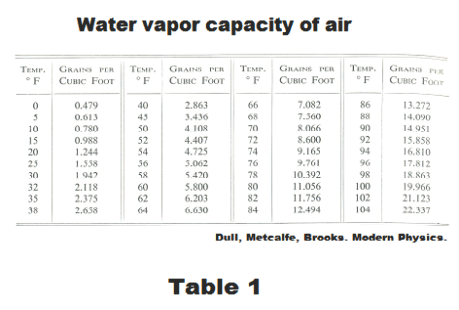
Water vapor capacity of air. The amount of moisture that air can hold when it is saturated is called its capacity. The water vapor capacity of air increases with increasing temperature and is usually measured in grains per cubic foot. See Table 1.
Absolute humidity. The amount of water vapor present in a unit volume of the atmosphere at a given time. It is usually expressed in g/m3, grains/ft3, or in lb/ft3.
Relative humidity. The ratio of the amount of moisture which air actually contains at a particular temperature to the amount it is able to hold (i.e. its capacity) at that temperature.
![]()
Dew point. The temperature at which the moisture in the air begins to condense.
As air cools it capacity for holding moisture drops and as it continues to cool its capacity for holding moisture may drop below the amount of moisture currently in the air. When this happens the excess moisture condenses. Depending on the temperature and other atmospheric conditions, the condensed water vapor will form dew, fog, rain, snow, frost, sleet, or hail. Before precipitation can occur, the temperature must be reduced to the dew point.
As air cools and its capacity for holding water vapor drops, the relative humidity increases. The dew point occurs when the relative humidity reaches 100%.
Determining dew point. The usual method for determining dew point is to cool a metal container with a bright, polished surface and to observe its temperature when the surface becomes clouded with condensed moisture.
Determining relative humidity. The most accurate method for determining relative humidity is by determining the dew point. The amount of moisture the air currently contains can be found by cooling it until it condenses. The temperature at which it condenses is its dew point and the amount of water vapor it holds at its dew point can be read from the table “Water vapor capacity of air” (Table 1 above). Its current water vapor capacity can be read from the same table and the relative humidity computed from the formula above.
Suppose the current temperature is 70o F and the dew point is found to be 50o F. From Table 1, the water vapor capacity of air at 70o is 8.066 grains/ft3 and the water vapor capacity at 50o is 4.108 grains/ft3. The relative humidity is then 4.108/8.066 = 0.51 or 51%.
Because the vapor pressure of water is approximately proportional to the mass of water vapor per unit volume, relative humidity can also be computed using a table of vapor pressures of water (Fig. 3 above) from the formula

Suppose the current temperature is 20o C and the dew point is found to be 10o C. From Fig. 3 above, the vapor pressure of water at 20o is 17.5 mm and the vapor pressure at 10o is 8.94 mm. Thus the relative humidity is 8.94/17.5 = 0.51 or 51%.
Simpler but less accurate methods of determining relative humidity include the wet-and-dry bulb thermometer and hair thermometer.
References
Dull, Metcalfe, Brooks. Modern Physics.
Sears, Zemansky. University Physics.
Schaum. College Physics.
Kittsley. Physical Chemistry.
Bailar. General Chemistry for Colleges.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life