Angular velocity and acceleration. Kinetic energy of a rotating body. Moment of inertia. Radius of Gyration. Work. Power. Torque. Angular momentum and impulse.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

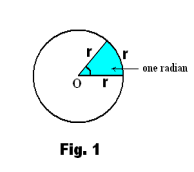
An important and much used unit of angular measure is the radian.

Def. Radian. One radian is that angle subtended at the center of a circle by an arc equal in length to the radius of the circle. See Fig. 1. There are 2π radians in a circle. One radian = 360^o/2π = 57.3^o.

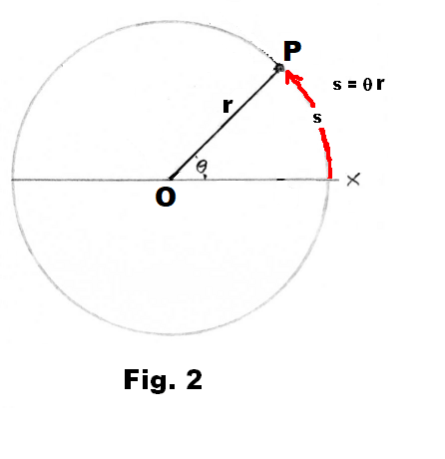
Def. Angular displacement. The angle in radians (degrees, revolutions) through which a point or line has been rotated in a specified direction about a specified axis. Example. In Fig. 2 the angular displacement of point P from the reference axis Ox is θ.

Def. Angular velocity. The time rate of change of angular displacement about an axis. It is expressed in radians/sec, degrees/sec, revolutions /sec (rps), and revolutions/min (rpm).

Angular velocity is regarded as a vector. It lies parallel to the axis of rotation and is pointed in the direction given by the right hand rule (curl the fingers of your right hand in the direction of rotation and your thumb points in the direction of the vector). As a vector it may be manipulated in accordance with the rules for manipulating vectors. Its vector nature is unimportant in many problems but is important in others.

Def. Angular acceleration. The time rate of change of angular velocity. It is usually expressed in radians per sec per sec (rad/sec²).

Since angular velocity is a vector, angular acceleration is also a vector quantity.

Angular relationships. Consider the motion of a particle P about a circle centered at O as shown in Fig. 2. If

r = the radius of the circle (in, ft, m, etc)

θ = the angular displacement of P in radians as measured counterclockwise from the positive x axis

s = linear distance traveled by P, measured from the positive x axis (in, ft, m etc.)

v = linear velocity (speed) of P (ft/sec, m/sec, etc.)

a = linear acceleration of P (ft/sec² , m/sec², etc.)

ω = angular velocity of P (rad/sec, rad/min etc.)

α = angular acceleration of P (rad/sec², rad/min², etc.)

f = frequency (rev/sec, rev/min, etc.)

T = period (Time required in sec, min, etc to make one complete revolution around the circle)

then the following relationships hold:

1) v = ds/dt

2) a = dv/dt

3) ω = dθ/dt

4) α = dω/dt

5) s = θr

6) v = ωr

7) a = αr

8) ω = 2πf

9) T = 1/f = 2π/ω = 2πr/v

Equations for uniformly accelerated angular motion. The equations for uniformly accelerated angular motion are completely analogous to those for linear motion. Let v_o and ω_o denote the initial linear and angular velocities respectively, and let v_t and ω_t denote the linear and angular velocities after time t. Then

v_t = v_o + at s = v_ot + ½ at² v_t² = v_o² + 2as

ω_t = ω_o + αt θ = ω_ot + ½ αt² ω_t² = ω_o² + 2αθ

If the body starts from rest, v_o = 0 and ω_o = 0 and

v_t = at s = ½ at² v_t² = 2as

ω_t = αt θ = ½ αt² ω_t² = 2αθ

Inertia and motion. A body at rest tends to stay at rest and a body in motion tends to stay in motion if there are no external forces exerting themselves on the body. If one were to give a marble a push on a smooth, level surface it would continue rolling in a straight line indefinitely were it not for frictional forces that cause it to come to a stop. The same is true for a block of wood. If you gave a block of wood a shove on a smooth, level surface it would slid forever were it not for frictional forces. If one were to start a child’s top spinning and set it down on a surface it would continue spinning indefinitely if it were not for frictional forces that bring it to a stop. The same is true for a gyroscope. There is an example in nature of a spinning object that does spin perpetually. It is our planet earth (or any planet that spins as it moves through space). In this case there no frictional forces to slow the movement.

Inertia. Inertia is the inherent property of a body that makes it oppose any force that would cause a change in its motion. A body at rest and a body in motion both oppose forces that might cause acceleration. The inertia of a body can be measured by its mass, which governs its resistance to the action of a force, or by its moment of inertia about a specified axis, which measures its resistance to the action of a torque about the same axis.

Kinetic energy of a rotating body and the moment of inertia. A body rotating about an axis possesses a kinetic energy of motion. The kinetic energy that it possesses is the sum total of all of the kinetic energies of all of the particles that make it up. A particle of mass m_i located at a distance r_i from the axis of rotation has kinetic energy given by ½ m_iv_i², where v_i is the speed of the particle. The total kinetic energy E_k of all the particles in the body will be given by

E_k = Σ ½ m_iv_i²

Remembering that v = ωr, the above becomes

E_k = Σ ½ m_ir_i²ω²

Since ω is the same for all particles in a rigid body, it can be factored out, and we get

E_k = ½ [ Σ m_ir_i²] ω²

The quantity Σ m_ir_i² is obtained dividing the body into a large number of infinitesimally small particles and doing the summation using integral calculus. This quantity is denoted by I

1] I = Σ m_ir_i²

and is called the moment of inertia of the body about that particular axis of rotation. The moment of inertia of a body is a measure of the resistance the body offers to any change in its angular velocity.

Note. Moment of inertia is usually expressed in slug-ft² in the engineering system, kg-m² in the mks system, and g-cm² in the cgs system.

The rotational kinetic energy for a body is then given by the formula

2] E_k = ½ Iω²

We see that it is exactly analogous to the formula for translational kinetic energy

K = ½ mv²

Radius of Gyration. In a rotating body there exists a point at some particular distance k from the axis of rotation at which the entire mass of the body can be assumed to be concentrated (i.e. where the body could be replaced by a point mass) without changing its moment of inertia. This distance k is called the radius of gyration of the body about that particular axis of rotation. Thus for a body of mass m and moment of inertia I about some specified axis of rotation the corresponding radius of gyration k is given by the formula I = mk² or

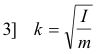
Parallel axis theorem. If the moment of inertia about an axis through the center of mass is known, the moment of inertia through an axis parallel to it is given by

4] I = I_G + mh²

where

I_G = moment of inertia about an axis through the center of mass

m = mass of the body

h = perpendicular distance between the two parallel axes

Moments of inertia for many bodies of simple geometric shape can be found in handbooks.

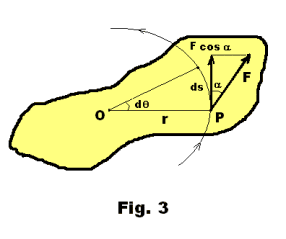
Work in rotational motion. Consider the body of Fig. 3, which is pivoted about an axis through O perpendicular to the plane of the figure. An external force F acts on the body at point P producing rotation. As the body rotates through a small angle dθ, point P moves a distance ds along its circular path, where ds = rdθ. The component of F in the direction of ds is F cos α. The work dW done by F is

dW = F cos α ds

dW = (F cos α) rdθ

Noting that the product (F cos α) r is the moment (or torque) M of force F about the axis, we have

5] dW = M dθ

which is the formula for the work done by a force acting on a rotating body. It is the rotational analogue of the formula W = F ds for translational motion.

[Note. In vector notation the work done is given by dW = M∙dθ ]

The work W done on a rotating body by a constant torque equals the product of the torque M and the angular displacement θ.

W = Mθ

Power in rotational motion. The power P in rotational motion is given by the formula

6] P = Mω

where M is the torque and ω is the angular velocity.

Derivation. This formula follows directly from 5]

[Note. In vector notation the power is given by P = M∙ω ]

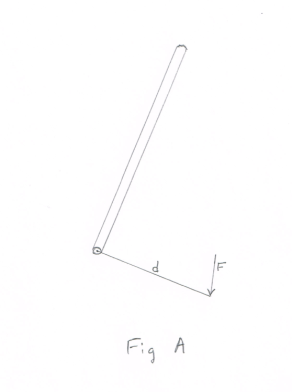
Torque. Torque is a twisting force that tends to produce rotation. See Fig. A. In Fig. A the force F is perpendicular to the plane containing the axis of rotation and d. Here Torque = F × d.

Torque is a vector quantity. Its direction is given by the following right hand rule: If the fingers of the right hand are wrapped in the direction of the twist, the thumb gives its direction. The torque about an axis is the moment of force about an axis. See Moment of a force, Couple

Theorem 1. Torque and angular acceleration. An unbalanced torque M, acting on a body of moment of inertia I about some fixed axis, produces in it an angular acceleration α in accordance with the formula

7] M = Iα

This is the rotational analogue of Newton’s second law, F = ma.

Derivation. The work done by a torque acting on a rotating body is given by the formula

dW = Mdθ

This work that is done on the body is equal to the increase in kinetic energy of the body i.e.

dW = d(½ Iω²) = Iωdω

Thus

Mdθ = Iωdω

Now the product is equal to the acceleration α, as we see from

Consequently 8] becomes

M = Iα

Def. Angular momentum of a particle about a fixed point. The angular momentum L of a particle P about some fixed point O is defined as

9] L = r × p

where r is the vector extending from O to P, p is the linear momentum of particle P, and × is the cross product.

This can be written as

10] L = r × mv

where m is the mass of particle P and v is its velocity.

Note that L represents the moment of the linear momentum of a particle and is sometimes called the moment of momentum of a particle.

Angular momentum of a collection of particles about a point. In a system containing multiple particles, the total angular momentum of the collection about a point O is obtained by adding all the angular momenta of the constituent particles about O:

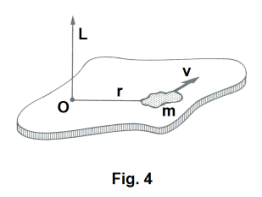
Fig. 4 shows a horizontal flat plate rotating about a vertical axis through point O. The angular momentum of each particle in the plate about O is

12] L = mvr

The angular momentum of the entire plate about O is then

13] L = ∑mvr

Since v = ωr, we have

14] L = ∑mr²ω

Since ω has the same value for all particles, this becomes

15] L = ω ∑mr²

and since ∑mr² = I , the moment of inertia, we have

16] L = Iω

Theorem 2. Angular momentum. The angular momentum of a body rotating about some fixed axis A is equal to its moment of inertia about A times its angular velocity about A i.e.

17] L_A = I_A ω

or more simply,

18] Angular momentum = Iω

The angular momentum Iω is the rotational analogue of the linear momentum mv.

Because angular velocity is a vector, angular momentum is also a vector. It lies parallel to the axis of rotation and is pointed in the direction given by the right hand rule. As a vector it may be manipulated in accordance with the rules for manipulating vectors.

Def. Angular impulse. The angular impulse of a rotating body is equal to its torque times the length of time the torque acts i.e.

19] Angular impulse = Mt

where

M = torque

t = length of time the torque acts

The angular impulse Ft is the rotational analogue of the linear impulse Ft.

Because torque is a vector, angular impulse is also a vector. It is parallel to the axis of rotation and pointed in the direction given by the right hand rule.

Relationship between angular impulse and angular momentum. Rewriting the equation relating torque and angular acceleration, M = Iα, we get

M = I dω/dt

20] M = d(Iω)/dt

and

21] Mdt = d(Iω)

These are the rotational analogues of the linear relationships F = d(mv) /dt and Fdt = d(mv).

From 20] and 21] we get the following:

Principle of the conversation of momentum. A rotating rigid body maintains a constant angular momentum unless acted upon by an unbalanced external torque.

Thus, because angular momentum is a vector quantity, both the magnitude and direction of the angular momentum (i.e. both the angular speed and direction of the axis of rotation) remain constant unless the body is acted upon by an unbalanced external torque. In other words, a rigid body set spinning on its axis will maintain its direction of rotation as well as its angular speed if no external torque acts on it.

Gyroscopic motion. Gyroscopic motion is the tendency of a rotating object to maintain the orientation of its rotation. A rotating object possesses angular momentum and this momentum must be conserved. The object will resist any change in its axis of rotation, as a change in orientation will result in a change in angular momentum.

Theorem 3. The change in angular momentum produced by an unbalanced angular impulse is equal to the angular impulse.

Thus if an unbalanced torque M acting for a time t on a body of moment of inertia I changes its angular velocity from an initial value ω₀ to a final value ω_t, then

Mt = I(ω_t - ω₀)

Analogous linear and angular formulas:

Linear: F = ma K.E. = ½ mv² Work = Fs Power = Fv

Angular: M = Iα K.E. = ½ Iω² Work = Mθ Power = Mω

Scalar quantities

angular displacement, θ

moment of inertia, I

rotational kinetic energy, E_k

radius of gyration, k

work, W

power, P

Vector quantities

angular velocity, ω

angular acceleration, α

torque or moment, M

angular momentum, L

angular impulse

__________________________________________________________

Torque and angular acceleration

M = Iα

M(lb-ft) = I(slug-ft²) × α(rad/sec²)

M(m-nt) = I(kg-m²) × α(rad/sec²)

M(cm-dyne) = I(g-cm²) × α(rad/sec²)

Kinetic energy of rotation

K.E. = ½Iω²

K.E. (ft-lb) = ½I(slug-ft²) × ω²(rad/sec)²

K.E. (joules) = ½I(kg-m²) × ω²(rad/sec)²

K.E. (ergs) = ½I(g-cm²) × ω²(rad/sec)²

Work

W = Mθ

W (ft-lb) = M(ft-lb) × θ(radians)

W (joules) = M(m-nt) × θ(radians)

Power

P = Mω

P(ft-lb/sec) = M(ft-lb) × ω(rad/sec)

P(watts) = M(m-nt) × ω(rad/sec)

References

Schaum. College Physics.

Sears, Zemansky. University Physics.

Semat, Katz. Physics.