Forces in mechanics. Resultant of general coplanar and spatial force systems.

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

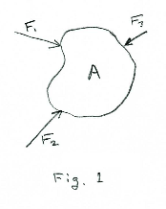
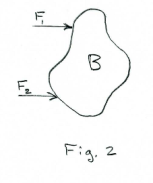
Forces in mechanics. In mechanics we deal with sets of forces acting on bodies and, in general, want to know the effect of those forces on the body or system. In Fig. 1 is a body in space being acted on by three forces: F₁, F₂ and F₃. In mechanics one asks such questions as: Given n forces acting on a body, what is their effect on the body in terms of translational and rotational motion? The effect they have depends not only on their magnitude and direction but also on their points of application. In Fig. 2 is shown two forces, F₁ and F₂, of equal magnitude and direction, but different points of application, acting on a body. It is obvious that although these forces have equal magnitudes and directions, their effect on the body is different. F₁ will tend to cause clockwise rotation and F₂ will tend to cause counterclockwise rotation. Thus in mechanics three items of information are important when specifying a force: (1) magnitude, (2) direction and (3) point of application.

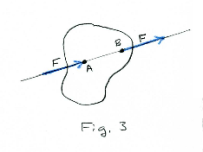
The action of a force on a body can be separated into two effects: external and internal effects. Internal effects are those of stresses and strains within the material of the body itself and is of concern in the subjects of strength of materials, elasticity, and plasticity. External effects are the effects on the body in terms of motion of the body or forces that may be exerted on the body by connected bodies. In the mechanics of rigid bodies only the external effects of forces are considered. When only external effects of forces are of interest, the effect of a force on a body is the same, wherever it is applied along the force’s line of action. In Fig. 3 the effect of the force F is the same whether it acts at point A or B. Its effect is the same wherever it acts on its line of action. This is called the principle of transmissibility. As a consequence, in problems involving rigid bodies it is sufficient to specify only the magnitude, direction and line of action of a force.

One of the important questions addressed in mechanics is the following: Given a system of n forces acting on a body, what simpler system would be equivalent to it in terms of effects on the body? For example, could the set of n forces be replaced by a single force that would produce the same effect? If so what is its magnitude, direction and line of action? We are thus led to the concept of a resultant.

Def. Resultant. The resultant of a system of forces is a simpler system of forces which has the same component of force in any direction and the same moment about any axis or point as the given system. The dynamic effect of the resultant acting on a rigid body will be the same as the effect of the given system of forces. If all forces are concurrent, the simplest form of the resultant is a single force. If all forces are parallel or coplanar they may be reduced to a single force or a single couple. In the general three-dimensional case both a force and a couple may be needed.

Def. Wrench. A force and a couple whose moment vector is parallel to the line of action of the force constitute a wrench. The resultant of any force system can always be reduced to a wrench.

The International Dictionary of Applied Mathematics

Resultant of a general coplanar force system. The resultant R of a general coplanar system of forces may be (1) a single force, (2) a couple in the plane of the system or in a parallel plane, or (3) zero. The resultant R corresponds to the vector sum of the forces of the system. Its x and y components are

1) R_x = Σ F_x , R_y = Σ F_y

where Σ F_x and Σ F_y are the algebraic sums of the x and y components, respectively, of the forces of the system.

The magnitude of R is given by

and the angle θ that it makes with the x axis is given by

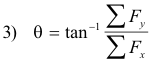
The line of action of R is found from

4) Rd = Σ M_O

where

O = any moment center in the plane

d = perpendicular distance from the moment center O to the resultant R

Σ M_O = the algebraic sum of the moments of the forces of the system with respect to O

Rd = the moment of R with respect to O

It should be noted that even if R = 0, a couple may exist with a magnitude equal to ∑M_O .

Resultant of a general spatial force system. The resultant of a general spatial force system is a force R and a couple C where R = Σ F, the vector sum of all the forces of the system, and C = Σ M, the vector sum of the moments of all the forces of the system. The value of R is independent of the coordinate system but the value of C depends on the center of moments chosen.

Erect an x-y-z coordinate system with origin O placed at some selected point inside or near the body. The origin O of the system will serve as the center of moments. The x, y, and z components of R are

5) R_x = Σ F_x , R_y = Σ F_y , R_z = Σ F_z

where Σ F_x , Σ F_y , and Σ F_z are the algebraic sums of the x, y and z components, respectively, of the forces of the system. The x, y, and z components of C are

6) C_x = Σ M_x , C_y = Σ M_y , C_z = Σ M_z

where Σ M_x , Σ M_y , and Σ M_z are the algebraic sums of the moments of the forces of the system about the x, y, and z axes respectively. The magnitudes of R and C are given by

and

If θ_x, θ_y, and θ_z are the angles that R makes with the x, y, and z axes respectively and α_x, α_y, and α_z are the angles that C makes with the x, y, and z axes respectively, then

cos θ_x = (Σ F_x)/R cos θ_y = (Σ F_y)/R cos θ_z = (Σ F_z)/R

cos α_x = (Σ M_x)/C cos α_y = (Σ M_y)/C cos α_z = (Σ M_z)/C

Derivation of R = Σ F and C = Σ M. The derivation of the formulas employs the idea of resolving a force into a force and a couple.

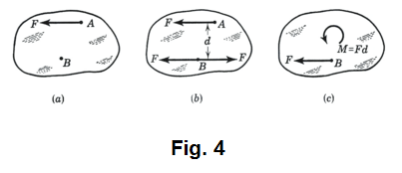
Resolution of a force into a force and a couple. Consider a body with a force F acting at point A as shown in Fig. 6a. At any other point B two equal and opposite forces F may be applied with no external effect on the body as shown in Fig. 6b. If these forces are parallel to the original force F, then a couple M = Fd is formed by the original F and the force F in the opposite direction at B. In Fig. 6c we see how the original force F at point A has been replaced by a force of the same magnitude and direction at point B and a couple. The magnitude of the couple is Fd, the product of the magnitude of F and the distance through which its line of action has been shifted. A force can always be replaced by an equal force having any parallel line of action and the corresponding couple. We now state this with vector notation in the following theorem:

Theorem 1. A single force F acting at point A may be replaced by an equal and similarly directed force acting at any other point B and a couple C = r×F where r is the vector from B to A.

Using Theorem 1 we proceed as follows:

Given: Forces F₁, F₂, ... , F_n.

1. Replace each given force F_i by a force of the same magnitude and direction emanating from the origin plus a couple.

This gives us n forces emanating from the origin and n couples. This new system is equivalent to the original system.

2. Take the sum of the moments about the origin of the n couples. Since one force in each couple passes through the origin, this is the equivalent of simply taking the sum of the moments about the origin of the n original forces. The sum of the moments about the origin of the n couples is equal to the sum of the moments about the origin of the n original forces.

The resultant R consisting of the vector sum of the n vectors emanating from the origin and the couple C given by the sum of the n couples (or equivalently, the sum of the moments of all the forces of the system) is equivalent to the original system.

References

J. L. Meriam. Mechanics, Part I- Statics

Faires, Chambers. Analytic Mechanics.

McLean, Nelson. Engineering Mechanics. (Schaum)

Eshbach. Handbook of Engineering Fundamentals.

The International Dictionary of Applied Mathematics. (D. Van Nostrand Co.)