Website owner: James Miller
Simple Harmonic Motion (SHM). Reference circle. Simple and compound pendulums.
Simple Harmonic Motion. Simple harmonic motion is a vibratory to-and-fro motion (an example being the bobbing of a weight suspended from a vertical stretched spring), in which the acceleration (a) on the body and the restoring force (F) acting on it are always directed towards some equilibrium point and are proportional to the displacement (x) from this point i.e. a = -cx where c is a constant.
Abbreviation. SHM
Whenever a body is distorted from its normal shape and then released, elastic restoring forces come into play and the body will vibrate about its normal equilibrium position, resulting in simple harmonic motion. Examples of this kind of motion are:
- the bobbing motion that results when a weight hanging from a spring is pulled down and released
- the vibrations of the strings or air columns of musical instruments
- the vibration of a bridge or building when impacted by a force
- the motion of the balance wheel of a watch or of a clock pendulum

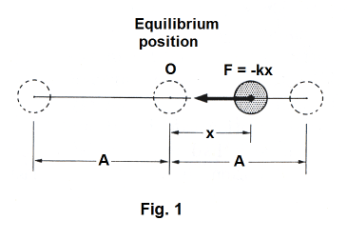
In Fig. 1 a vibrating body oscillates between a maximum position of x = A and a minimum position of x = -A in accordance with an elastic restoring force that is proportional to its distance from the point of equilibrium O, and directed toward O
1) F = -kx
where k is the force constant and A is the amplitude of the vibration. At a distance x from the point of equilibrium O, the body experiences a force of F = -kx. The body obeys Newton’s second law F = ma, where m is the mass of the body, so
2) F = -kx = ma
or
![]()
The amount of maximum displacement A is called the amplitude of the vibration.
It can be shown that the displacement x, velocity v, and acceleration a of the body at any given time t is given by
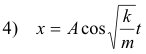
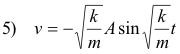
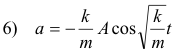
Most vibrating bodies are governed by a restoring force law of the type F = -kx and any body that is governed by that law undergoes what is called Simple Harmonic Motion. A model for Simple Harmonic Motion is found in the Reference Circle described below and that circle is very useful in analyzing and understanding the motion of a vibrating body.
Def. Period. The time required for one complete vibration (time required to make one round trip). For a particle (or point) moving around a circle, the time required to make one complete revolution.
Def. Frequency. The number of vibrations made per second (or other unit of time). For a particle moving around a circle, the number of revolutions made per second (or other unit of time).
Def. Angular velocity. The rate at which a body rotates about an axis or a particle in a plane moves about a fixed point (origin) expressed in rad/sec, rad/min, etc.
● The period T, frequency f, and angular velocity ω are related by:
ω = 2πf
T = 1/f = 2π/ω
Def. Displacement. The distance of the vibrating body at any instant of time from its normal position of rest (equilibrium point).
Reference circle. If a point P moves at constant speed around a circle of radius A called the reference circle, then the motion of the projection Q of point P on the diameter of this circle is simple harmonic motion. See Fig. 2. The motion of point Q corresponds to the harmonic
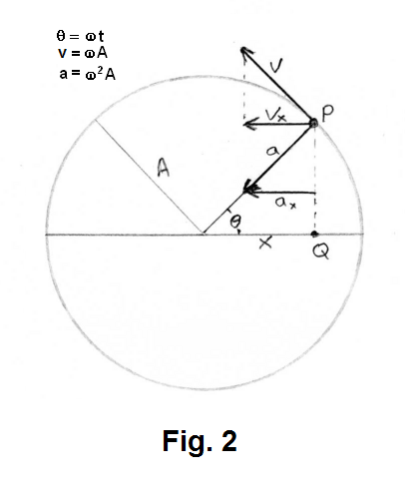
motion of a vibrating body that vibrates with an amplitude of A. The coordinate of Q is always equal to the x-coordinate of P, the velocity of Q is equal to the x-component of the velocity of P, and the acceleration of Q is equal to the x-component of the acceleration of P.
Assume that point P moves around the reference circle with the constant angular velocity ω. The velocity of P equals ωA. At any time t the angle θ is given by θ = ωt.
The location of Q ( i.e. the x-coordinate of point P) at time t will be given by
7) x = A cos ωt
See figure. The velocity of Q is obtained by taking the derivative of 7) with respect to t
8) vx = -ωA sin ωt
The acceleration of P is its radial acceleration, a = ω2A, directed toward the center of the circle. Taking the derivative of 8) with respect to t we get
9) ax = -ω2A cos ωt
which is the x-component of a, or equivalently,
10) ax = -ω2 x
The angular velocity ω of P in rad/sec, is related to the frequency f, by ω = 2πf. The above formulas can thus be written
11) x = A cos 2πft
12) vx = -2πfA sin 2πft
13) ax = -4π2f2x = -4π2f2 A cos 2πft
These three formulas give the displacement x, velocity v, and acceleration a of a body undergoing simple harmonic motion. They correspond to the formulas 4), 5) and 6) above. The concepts of a restoring force F and force constant k do not come into play in connection with the Reference circle. In a vibrating body problem, since the acceleration of the body is given by
a = -4π2f2x,
the restoring force F is given by
14) F = ma = -4mπ2f2x
and the force constant k is given by
15) k = -F/x = 4mπ2f2
Period. The period in simple harmonic motion can be given by
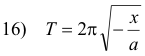
or
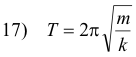
which can be derived from 13) and 15) above using T = 1/f.
Simple and compound pendulums. As simple pendulum consists of a body of small dimensions suspended by an inextensible weightless string. A compound pendulum (also called physical pendulum) is any swinging rigid body. A compound pendulum corresponds to a real pendulum as opposed to a simple pendulum in which all the mass is assumed to be concentrated at a point.
Period of a simple pendulum. The period of a simple pendulum is given by
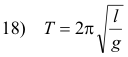
where l is the length of the pendulum and g is the acceleration of gravity.
Period of a compound pendulum. The period of a compound pendulum is given by
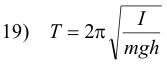
where
m = mass of the pendulum
I = its moment of inertia about a transverse axis at the point of suspension
h = the distance of its center of gravity from the point of suspension
If we equate the periods of the simple and compound pendulum, we get
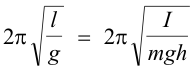
or
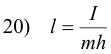
Thus a compound pendulum has the same period as a single pendulum whose length is l = I/mh. This length is called the length of an equivalent simple pendulum.
A compound pendulum vibrates as if its mass were concentrated at a single point at a distance l (= I/mh) from the axis of suspension. This point is known as the center of percussion or center of oscillation. If the pendulum is struck at the center of percussion, it rotates about the axis of suspension without jarring it, i.e. without tending to give the axis a motion of translation.
Angular simple harmonic motion. Angular simple harmonic motion, or simple harmonic motion of rotation, is periodic, oscillating angular motion in which the restoring torque is (1) proportional to the angular displacement and (2) opposite in direction to the angular displacement. If a body suspended from a vertical wire is twisted about the wire in a horizontal plane and released, it executes rotary (angular) simple harmonic motion.
Schaum. College Physics. p. 84
Torsion constant K. The torsion constant K for angular harmonic motion is given by
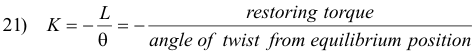
where K is positive since L and θ are oppositely directed.
Period of a torsion pendulum. The period of a torsion pendulum is given by the formulas
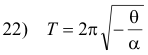
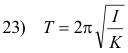
where
θ = angular displacement from equilibrium position
α = angular acceleration
I = moment of inertia of vibrating body about the axis of rotation
The period T is given in seconds if (1) I is in slug-ft2 and K is in lb-ft/radian or (2) I is in Kg-m2 and K is in m-nt/radian.
Since θ and α are opposite in sign, -θ/α is positive.
References
Schaum. College Physics.
Sears, Zemansky. University Physics.
Semat, Katz. Physics.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life