Parallelogram law for adding velocities, accelerations and forces

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

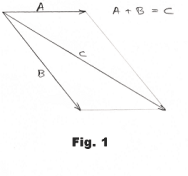
Certain quantities in physics (e.g. forces, displacements, velocities, accelerations) are viewed as vectors and treated according to the laws for manipulating vectors. What is the rational for treating them in this way? How do we know they obey the laws for vectors? Vectors are added by the parallelogram method. How do we know what we are doing is valid? For example, we are told that the resultant of two forces acting at an angle upon a given point is equal to the diagonal of a parallelogram of which the two forces are sides. See Fig. 1. How do we know this is true for real forces? We are told that any force can be decomposed into a sum of forces whose vector sum is that force. How do we know this is true?

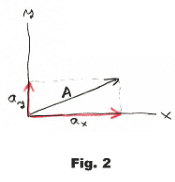
Displacements. That the parallelogram method is the correct method for adding displacements is obvious. See Fig. 2. Traveling the distance A is equivalent to traveling the distance a_x, then traveling the distance a_y.

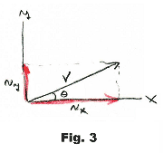
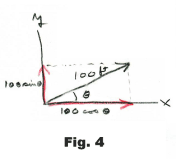
Velocities. That the parallelogram method is the correct method for adding velocities follows directly from the fact that it is the correct method for adding displacements. In Fig. 3, if the velocity V is 100 ft/sec then the velocity in the x direction will be v_x = 100 cos θ and the velocity in the y direction will be v_y = 100 sin θ. Why? In one second the particle moves 100 ft as shown in Fig. 4. Then its displacement will be 100 cos θ in the x direction and 100 sin θ in the y direction. Thus its velocity in the x direction is v_x = 100 cos θ and the velocity in the y direction is v_y = 100 sin θ.

Accelerations. That the parallelogram method is the correct method for adding accelerations also follows directly from the fact that it is the correct method for adding displacements. We use the same kind of logic as we used with velocities.

Forces. Newton’s second law states that for any unbalanced force F,

F = ma

where m is mass and a is acceleration. If we agree that it is valid to add accelerations by the parallelogram method, then it must be valid to add products of the form “ma” by the parallelogram method. We can then reason that it must be legitimate to add forces by the parallelogram method.

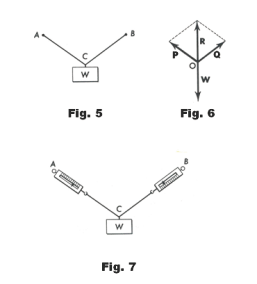
That the parallelogram method gives the correct answers when adding forces can be confirmed by experiments using spring scales. For example, consider Fig. 5 in which a weight W hangs from a ceiling by two cords AC and BC. We can compute the tensions P and Q in the two cords by using the parallelogram method. We compute the two forces P and Q that are equivalent to the force R as shown in Fig. 6, where R is equal in magnitude to W. We can then insert spring scales in the cords AC and BC as shown in Fig. 7 and compare the readings with the numbers obtained by the parallelogram method.

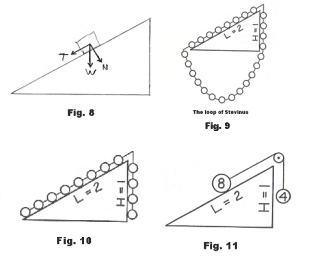
It is noteworthy, however, that Stevinus (1548 - 1620) essentially derived the parallelogram method for adding forces by ingenious rational argument alone, without resorting to experiment. Let us consider his approach and arguments. Consider a block of weight W resting on a frictionless inclined plane as shown in Fig. 8. It is desired to find expressions for the force T parallel to the incline and the normal force N perpendicular to the incline. To this purpose, Stevinus conceived of a wedge over which was draped a loop of balls, all of equal size and weight, as shown in Fig. 9. Supposing no friction, he asked if the loop would move. He then answered that it would not move for if it moved, it would continue moving, and that would constitute perpetual motion, a possibility he judged to be absurd. He then observed that the hanging portion of the chain, which pulls equally at each end, can be removed without disturbing the equilibrium. We are thus left with the situation shown in Fig. 10. In Fig. 10, the hanging portion of the chain balances the portion that rests on the incline. The weights of these two sections of chain are proportional to their lengths and thus to the vertical height H and to the length L of the incline respectively. In the example shown, there are eight balls on the incline and four balls that hang vertically. Suppose the balls weigh one pound each. Now imagine that the balls on the incline are combined into a single ball equal to their aggregate weight, and similarly for the balls that hang vertically, and that these two new balls are connected by a rope running over a pulley as shown in Fig.11. We see that the four pound ball hanging vertically exactly balances the eight pound ball resting on the incline.

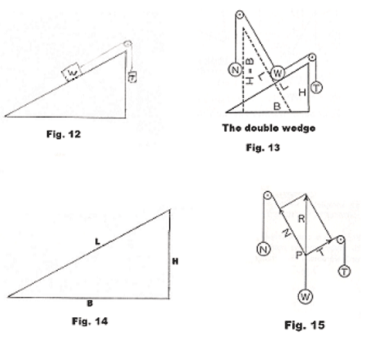
Let us now consider Fig. 12 in which a weight T is counterbalancing the block of weight W on the incline (where we note that T represents the component of W in the direction of the slope as shown in Fig. 8). What expression can we write relating the weight T to other variables? Considering Figures 10 and 11 and the fact that in Fig. 10 the weights of the two links of the chain are proportional to their lengths and thus to the vertical height H and to the length L of the incline respectively, Stevinus arrived at the following relationship between the variables T, W, L and H:

where the weight W of the block corresponds to the weight of the ball on the incline and the force T corresponds to the weight of the ball that hangs vertically. In other words,

Stevinus then found an expression for the normal force N by applying the same kind of reasoning to a different imagined wedge shown in Fig. 13 in dashed lines. Let B be the length of the base of the old wedge. See Fig. 14. Then the height of this new wedge is made equal to B and the inclined planes are made perpendicular to each other. It can then be shown that the two triangles are equal. The base of the new wedge is equal to the height H of the old wedge. The force down the new inclined plane is then equal to N and with a rope running over a pulley, the weight W is counterbalanced by a weight N. Using this line of reasoning, Stevinus gave the expression for N as

or, equivalently,

Stevinus went further. The weight W in Fig. 13 is completely supported by two ropes. The wedges are superfluous and can be removed. We now have a situation equivalent to that shown in Fig. 15. Here we have three forces in equilibrium and if we represent the forces by vectors we see that force R, a force equal in magnitude to W but opposite in direction, can be obtained from the forces N and T by the method of parallelograms. Here R is the vector sum of the vectors N and T. It is the diagonal of a rectangle of which N and T form the sides and is called the resultant of the forces N and T.

Here N and T are at right angles to each other but this is not necessary, they can be at an oblique angle, and the resultant is the diagonal of a parallelogram.

References

Morton Mott-Smith. Principles of Mechanics Simply Explained. Dover.