Moment of a force, Couple

SolitaryRoad.com

Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

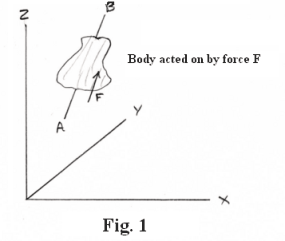
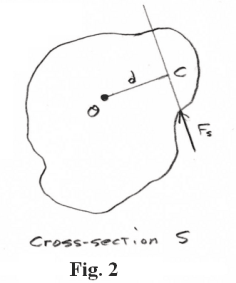
Moment of a force (or torque) about an axis. In Fig. 1 a body that is free to rotate about an axis AB is acted on by a force F. We wish to find the moment of F about the axis AB. In Fig. 2 is a cross-section S taken perpendicular to the axis of rotation AB with O indicating the axis. The force F_s shown in the figure is the component of F lying in the cross-sectional plane S (F is decomposed into a component parallel to the plane and a component perpendicular to the plane). The distance d from the axis O to the line of action of F_s is called the force arm or moment arm.

Moment of a force (or torque) about an axis. The moment of force F about the axis AB is defined as the product of the moment arm and force F_s i.e.

Moment of F = d × F_s

The moment of force about an axis is a measure of the effectiveness of the force in producing rotation about the axis. The moment is often considered to be a vector quantity. In this case the moment of F is defined as

M = × F_s

where is the vector from the axis O to point C in Fig. 2. It is a vector perpendicular to the plane S with a direction given by the right hand rule for cross products.

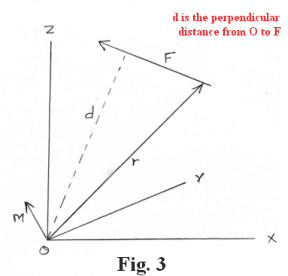
Moment of a force about a point. The moment of a force F about a point O is the vector quantity r × F where r is the position vector from the moment center O to any point on the line of action of the force F. See Fig. 3. Its magnitude is the product of the magnitude of F and the perpendicular distance from O to the line of action of F. Its direction is perpendicular to the plane determined by O and the line of action of F.

Denote the moment of F about O by M_O(F) and let

1) r = xi + yj + zk, F = F_xi + F_y j + F_z k, M_O(F) = M_xi + M_y j + M_z k

Then, by definition

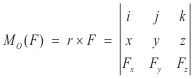
Expanding the determinant we get

M_O(F) = i(F_zy - F_yz) + j(F_xz - F_zx) + k(F_yx - F_xy)

Comparing this expression with that for M_O(F) in 1) above, we have

M_x = F_zy - F_yz, M_y = F_xz - F_zx, M_z = F_yx - F_xy

It can be shown that M_x, M_y, and M_z are the respective moments of the force F about the x, y, and z axes as defined by Def. 1 above (moment of force about an axis). It is this fact that makes the moment of force about a point, M = r×F, so very useful.

Def. Moment center. The point about which moments are computed. Symbolizing moment as r × F, the moment center is the origin from which the position vector r to any point on the line of action of the force F is measured.

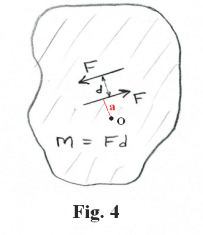
Def. Couple. A couple is a pair of parallel forces, equal in magnitude and opposite in direction. See Fig. 4. Two such forces cannot be combined into a single force since their sum in every direction is zero. Their sole effect is that of producing torque, a tendency towards rotation.

Moment of a couple. The moment of a couple about some moment center is given by the sum of the moments of the two forces constituting the couple about that moment center. Fig. 4 shows a couple consisting of two forces in the plane. The moment of the couple about point O (an axis of rotation perpendicular to the plane) is given by

M_O = (a + d)F - aF

M_O = Fd .

To find the moment of a couple in three-dimensional space we can employ the concept of the moment about a point. Consider Fig. 5. The moment C of the couple shown there, consisting of two opposing parallel forces F separated by a distance d, is given by

C = M_o(F) + M_o(-F) = r₁ × F + r₂ × -F = (r₁ - r₂) × F

C = a × F

where a = r₁ - r₂

By definition of the cross product, the magnitude of C is |a × F| = aFsin θ and a sin θ is equal to d,

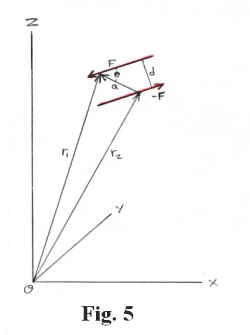
the perpendicular distance between the forces.

The moment M of a couple is a vector perpendicular to the plane of the two forces. Its magnitude is Fd where F is the magnitude of the forces and d is the perpendicular distance between them. Its direction is given by the right-hand convention: Curl the fingers of the right hand in the direction in which the couple tends to cause rotation and the thumb points in the direction of the couple.

Couples obey all the laws of vectors. The magnitude of a couple is the same for all moment centers.

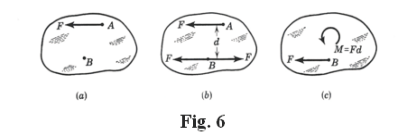
Resolution of a force into a force and a couple. Consider a body with a force F acting at point A as shown in Fig. 6a. At any other point B two equal and opposite forces F may be applied with no external effect on the body as shown in Fig. 6b. If these forces are parallel to the original force F, then a couple M = Fd is formed by the original F and the force F in the opposite direction at B. In Fig. 6c we see how the original force F at point A has been replaced by a force of the same magnitude and direction at point B and a couple. The magnitude of the couple is Fd, the product of the magnitude of F and the distance through which its line of action has been shifted. A force can always be replaced by an equal force having any parallel line of action and the corresponding couple. We now state this with vector notation in the following theorem:

Theorem1. A single force F acting at point A may be replaced by an equal and similarly directed force acting at any other point B and a couple C = r×F where r is the vector from B to A.

It follows that a given force and couple which act in the same plane may be combined to yield a single equal force having a unique line of action.

References.

McLean, Nelson. Engineering Mechanics. (Schaum)

Meriam. Mechanics, Part I - Statics.