Website owner: James Miller
GEOMETRIC PROOF OF THE LAW OF THE LEVER

A lever consists of a rigid bar which is free to turn about a fixed point called the fulcrum.
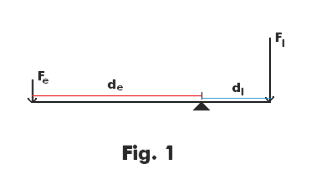
The law of the lever states that the equilibrium condition of balance exists when the effort force Fe multiplied by the length de of the effort arm is equal to the load force Fl multiplied by the length dl of the load arm i.e. when
Fe de = Fl dl .
See Fig. 1. This law can be derived by a geometric argument as follows:
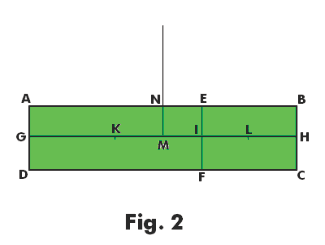
Proof of the law of the lever. Consider a uniform bar ABCD suspended by its middle point M so that it balances. See Fig. 2. Imagine that it is divided at EF into two parts AEFD and EBCF whose middle points are at K and L. Let WAEFB be the weight of AEFD and WEBCF be the weight of EBCF. Then the weights of AEFD and EBCF are proportional to GI and IH i.e.
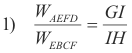
and may be supposed to be concentrated at K and L. Referring to Fig. 2, the law of the lever then states that
![]()
or
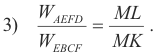
We will prove that this assertion 3) is true by showing that
![]()
Proof. Denote the length GH of the bar by
![]() and the distance MI by
and the distance MI by
![]() i.e.
i.e.
![]()
![]()
We then find the distances GI, IH, ML, and MK in terms of
![]() and
and
![]()
![]()
![]()
![]()
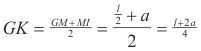
![]()
Thus
![]()
![]()
and so
![]()
Hence,

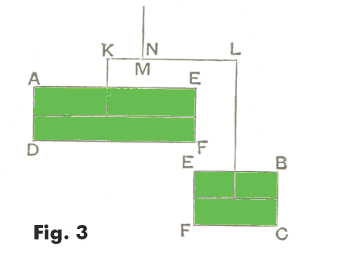
Fig. 3 shows that the weights may be hung at any depth below the bar, and that any equal weights may be substituted for the parts of the bar.
With some modifications this proof was given by Stevinus of Bruges, Galileo and Lagrange.
Reference.
Cox. Mechanics.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life