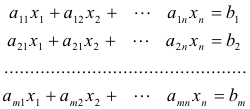
Website owner: James Miller
Matrices, Operations on matrices, Algebraic laws obeyed by matrices
Motivation for the concept of a matrix.
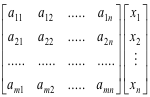
Systems of simultaneous linear equations crop up in many places in applied mathematics and numerical procedures for solving them is of great interest. The concept of a matrix arises directly out of the problem of solving systems of simultaneous linear equations. Consider the system of m equations in n unknowns
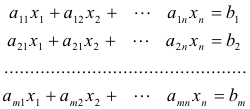
The process of finding a solution to this system involves performing a series of operations on that array of numbers that defines it i.e. on the array
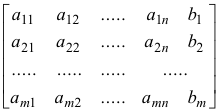
Thus the technique reduces to performing operations on blocks or arrays of numbers. And thus a mathematical interest in arrays of numbers and the idea of doing operations on them. We call an array of numbers a matrix.
Matrix. A matrix is a rectangular array of numbers which we enclose in brackets to show that it is a matrix. The following are matrices:
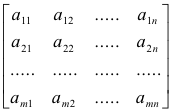

The definition of a matrix has been broadened to also include arrays whose elements are functions. Thus the official definition of a matrix is that it is an array whose elements are either numbers or functions.
A matrix may consist of only a single element, a column of elements, a row of elements or a rectangular array of elements.
These rectangular arrays called matrices have come to be regarded as mathematical entities in themselves. Operations of addition and multiplication have been defined for them and they are manipulated in a manner similar to the way numbers and symbols are manipulated in classical algebra. They are manipulated as number-like objects in what is called matrix algebra (in analogy to classical algebra).
The elements of a matrix may be complex numbers, real numbers or numbers from some other number field. If all the elements of a matrix A are in a field F, we say that “A is over F”. Thus we speak of a matrix A as being over the field of real numbers, the field of complex numbers, etc..
Order or dimension of a matrix. The order or dimension of a matrix is given by stating the number of rows and then the number of columns in the matrix. A matrix of m rows and n columns is said to be of order or dimension “m by n” or m x n.
Equal matrices. Two matrices A and B are said to be equal if and only if they have the same order and each element of one is equal to the corresponding element of the other (i.e. if and only if one is a duplicate of the other).
Zero Matrix. A matrix, every element of which is zero.
Addition of matrices. If A and B are two m x n matrices their sum is defined as the m x n matrix C where each element of C is the sum of the corresponding elements of A and B. Two matrices can be added if and only if they are of the same order, in which case they are said to be conformable for addition. Thus if

and
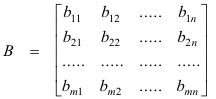
then
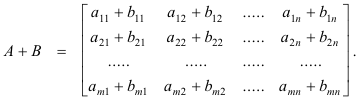
Subtraction of matrices. If A and B are two m x n matrices their difference A - B is computed as A + (-B) where -B is B with the signs of all its elements reversed. Two matrices can be subtracted if and only if they are of the same order, in which case they are said to be conformable for subtraction.
Concept of multiplying two matrices. An idea of multiplying two matrices has been developed and defined in such a way as to allow us to write the equations of a linear system in abbreviated form.
Let us now give the meaning of the matrix product AX of an m by n matrix A with an n-element
column matrix X. Let A and X be the matrices
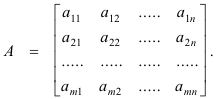
and
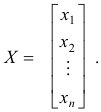
The product
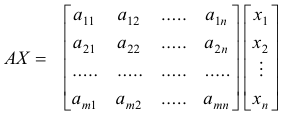
is the m-element column matrix
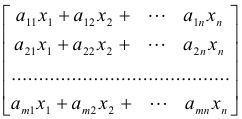
in which the i-th element is the m-dot product of the i-th row of matrix A and the column matrix X i.e.
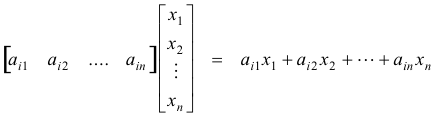
where
![]()
is the i-th row of the matrix A (we regard the i-th row of matrix A and the column matrix X as n-vectors) .
With this definition we see that a system of linear equations
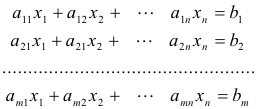
can be written in the matrix form
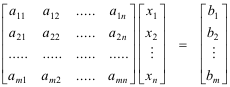
or, more concisely, as
AX = B
if we set
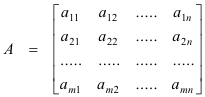
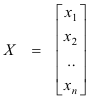
and
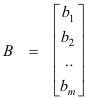
We are now ready to give the general definition of the product of two matrices.
Product of two matrices. The product AB of two matrices is defined only for the case in which the number of columns of A is equal to the number of rows of B, in which case the matrices are said to be compatible for multiplication. Let A be an m x n matrix and B be a n x q matrix. Then the product AB is defined as the m x q matrix Q whose element in the i-th row and j-th column is given by the m-dot product of the i-th row of matrix A and the j-th column of matrix B. In other words, element qij of Q is given by the m-dot product
qij = Ri ∙Cj
where Ri is the i-th row of A and Cj is the j-th column of B ( Ri and Cj being viewed as n-vectors).
Motivation behind the definition of the product of two matrices. What motivated this particular definition of the product of two matrices? In part the motivation was probably a generalization on the definition of the product of a matrix and a column vector
as defined above. There are also other facts that probably played a role as motivation. To name two:
Fact 1. If A and B are two n x n matrices and the determinant of A is |A| and the determinant of B is |B| then |AB| = |A||B| i.e. the determinant of AB is equal to the product of the determinants of A and B. This would presumably not be true if matrix multiplication were defined in any other way.
Fact 2. Let
(1)
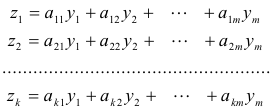
and
(2)
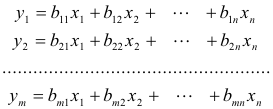
If we substitute in (1) the expressions for y1, y2, .... ,ym in terms of x1, x2, .... ,xn we obtain
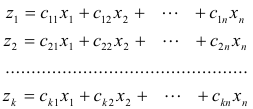
where the matrix of coefficients
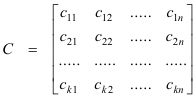
is given by
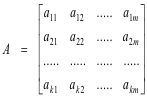
C = AB
where
and
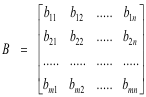
Multiplication of a matrix by a scalar. Let c be any number (i.e. any real or complex number) and A be an m x n matrix. The product cA = Ac is defined as the matrix obtained by multiplying each of the elements of A by c. Thus if

then
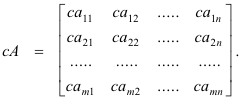
Algebraic laws obeyed by matrices. The following are the algebraic laws obeyed by matrices where A, B and C below are matrices and a and b are numbers. All matrices are assumed to be conformable for the operation.
1. A + B = B + A (commutative law for addition)
2. (A + B) + C = A + (B + C) (associative law for addition)
3. a(A + B) = aA + aB (distributive laws for multiplication
4. (a + b )A = aA + bA by a number)
5. There exists a “null” matrix
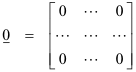 (Existence of null element for addition)
(Existence of null element for addition)
such that A + 0 = A for every matrix A.
6. a0 = 0A = 0; conversely, if aA = 0 , then a = 0 or A = 0 (existence of null element for
multiplication by a scalar)
7. For every matrix A there exists an opposite matrix -A such that A + (-A) = 0 (existence of an additive inverse)
8. (A + B)C = AC + BC (distributive laws for multiplication)
C(A + B) = CA + CB
9. (AB)C = A(BC) (associative law for multiplication)
10. (aA)B = A(aB) = a(AB) (associative law for multiplication
by a number)
There are some peculiarities in regard to operations on matrices which are worthy of note:
1. In general AB is not equal to BA (the commutative law for multiplication doesn’t hold).
2. AB = 0 does not necessarily imply A = 0 or B = 0 .
3. AB = AC does not necessarily imply B = C.
4. In general there is no multiplicative inverse. A multiplicative inverse exists only in the case of non-singular square matrices.
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life