Preliminary definitions, conventions and notations. n-vectors, n-space, dot products, m-dot products

SolitaryRoad.com

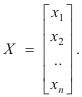
Website owner:  James Miller

[ Home ] [ Up ] [ Info ] [ Mail ]

Preliminary definitions, conventions and notations. N-vectors, n-space, dot products, m-dot products

List of Symbols and notation. We shall employ the following symbols and notation:

R – set of all real numbers

C – set of all complex numbers

R^# – set of all rational numbers

I – set of all integers

I⁺ – set of all positive integers

V_n(F) – n-space over field F

Rⁿ – real n-space

Cⁿ – complex n-space

Concept of an n-vector. In the field of physics some things such as temperature, volume, distance, time and speed possess only “magnitude”. Other things such as forces, velocities and accelerations possess both magnitude and direction. Those quantities which possess only magnitude we represent by real numbers called scalars and those which have both magnitude and direction we represent by things we call “vectors” where vectors are conceived of as “directed line segments” (arrows). In two dimensional space a vector, considered to extend from the origin of a rectangular Cartesian coordinate system to some point in the plane, is represented by two numbers, called its components. The two numbers by which it is represented correspond to the coordinates of its endpoint. Similarly in three dimensional space vectors are considered to extend from the origin of a rectangular x-y-z coordinate system to some point in space and are represented as triples of three numbers corresponding to the coordinates of their endpoints. Thus the vectors of two dimensional space have come to be identified with number doublets and the vectors of three dimensional space as number triplets. With time and a certain generalizing and abstracting process a vector of two dimensional space has come to be defined simply as a number doublet. Similarly a vector of three dimensional space has come to be defined as simply a number triplet. Then with a little more generalizing and abstracting the idea of an n-dimensional vector is conceived. An n-dimensional vector is simply an n-tuple of numbers. Its components are assumed to come from some field (as the field of real or complex numbers). An n-dimensional vector, called an n-vector, is viewed as a single member of a set of vectors called n-space.

N-space. The usual concept of space, what most people understand by the word “space”, is a continuum extending in three directions. The concept of n-space is different, necessarily different. The concept of n-space is that of a set, a collection. It is that set or collection consisting of all possible n-tuples

(x₁, x₂, ..... , x_n)

where each component x_i of the n-tuple may assume any value in the continuum - ∞ < x_i < ∞ . What we have just described is n-space for the field of real numbers. There can be n-spaces for fields other than the field of reals. There can, for example, be an n-space for the field of complex numbers, the field of rational numbers, etc..

N-space for the case of real numbers consists of the set of all n-tuples of real numbers. It represents the totality of all possible n-tuples of real numbers.

Let us consider the concrete case of 4-space. 4-space for real numbers is that set consisting of all possible quadruples (a, b, c, d) where a, b, c and d are real numbers. For the first number a in the quadruple there is the entire continuum - ∞ < a < ∞ of possible candidates, for the second number b there is the same continuum - ∞ < b < ∞ of possible candidates, and likewise for numbers c and d. The set thus contains an infinity of elements. The concept, however odd, unusual or different it may seem, is a useful one. We then view any particular quadruple (a, b, c, d) as a vector from this “space” of vectors.

In the same way, the 4-space for complex numbers consists of the set of all possible quadruples of complex numbers (a, b, c, d) .

Utilizing the concept of an n-space, any particular n-tuple of real numbers is viewed as a vector of real n-space. Any n-tuple of complex numbers is viewed as a vector of complex n-space. N-space for real numbers is denoted by V_n(R). N-space for complex numbers is denoted by V_n(C). N-space for an arbitrary field F is denoted by V_n(F).

Def. V_n(F). The set of all n-tuples with components from field F.

Def. Real n-space. The n-space V_n(R). Also called Rⁿ.

Def. Complex n-space. The n-space V_n(C). Also called Cⁿ.

Def. n-vector. An n-tuple such as X = [x₁,x₂, ... ,x_n] with components from some field F. It is regarded as a vector in V_n(F). The n elements are referred to as the components of the vector. The definition is a generalization of the concept of the three-component vectors of three dimensional space. Vectors may be written in either row form or column form i.e.

X = [x₁,x₂, ... ,x_n]

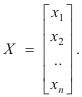
When we speak of vectors with elements from some field F we often refer to them as “vectors over field F”.

Def. Sum of n-vectors. The sum of two n-vectors is obtained by adding their corresponding components. The sum of two n-vectors X = [x₁,x₂, ... ,x_n] and

Y = [y₁,y₂, ... ,y_n] is defined as X + Y = [x₁ + y₁, x₂ + y₂, ... ,x_n + y_n].

Def. Multiplication by a scalar. The product of a scalar c and a vector X is the vector obtained by multiplying each component of X by c. Thus for a n-vector X = [x₁,x₂, ... ,x_n] the product cX is defined as cX = c [x₁,x₂, ... ,x_n] = [cx₁,cx₂, ... ,cx_n] .

Def. Real vector. A vector whose components are real numbers.

Def. Complex vector. A vector whose components are complex numbers.

Example 1. Let Q be the set of all real 2-tuples (x₁, x₂). This set is Real 2-space, V₂(R). It is the set of all vectors extending from the origin to all points of the plane.

Example 2. Let Q be the set of all real 3-tuples (x₁, x₂, x₃). This set is Real 3-space, V₃(R). It is the set of all vectors extending from the origin to all points of three dimensional space.

Example 3. Let Q be the set of all real 4-tuples (x₁, x₂, x₃, x₄). This set is Real 4-space, V₄(R).

Conjugate of a complex number. The conjugate of the complex number z = a + bi is a - bi . Two numbers of the type a + bi and a - bi, where a and b are real, are called conjugate complex numbers. We will denote the conjugate of a complex number by an over-bar. Thus the conjugate of the complex number z will be denoted by .

Example. The numbers 5 + 2i and 5 - 2i are conjugates.

We shall generally be dealing with vectors and matrices whose elements are from the field of complex numbers or the field of real numbers. We will now give the general definition of a dot product of two n-vectors.

Def. Dot Product (or inner product or scalar product). Let X = [x₁,x₂, ... ,x_n] and Y = [y₁,y₂, ... ,y_n] be complex vectors. Then their dot product is defined as

where over-bars refer to conjugates. Since real vectors are a special case of complex vectors, this definition also applies to real vectors. For the case of real vectors the definition reduces to

X∙Y = x₁y₁ + x₂y₂ + ... + x_ny_n

The dot product is also called the inner product and the scalar product. The three terms are used interchangeably.

We will now define a variation of the dot product. This definition is our own. We will find it useful in defining with more clarity certain concepts (such as the product of two matrices).

Def. M-Dot Product (Modified Dot Product). Let X = [x₁,x₂, ... ,x_n] and Y = [y₁,y₂, ... ,y_n] be either real or complex vectors. Then their m-dot product is defined as

X∙Y = x₁y₁ + x₂y₂ + ... + x_ny_n

The m-dot product is the same as the dot product for the case of real vectors. It is a different product than the dot product for the case of complex vectors.

References.

Ayres. Matrices (Schaum).