Website owner: James Miller
Solid geometry definitions. Dihedral, polyhedral angle. Prismatic, cylindrical, pyramidal, conical surface. Polyhedron, prism, parallelepiped, cylinder, pyramid, prismatoid. Frustum. Conic section. Circle, axis, pole of a sphere. Zone. Polar triangle. Spherical polygon, triangle, sector.
Foot of a line. The point of intersection of a straight line and a plane.

Line perpendicular to a plane. A line is perpendicular to a plane if it is perpendicular to every line in the plane passing through its foot.
Parallel lines and planes. A line and a plane are parallel if they do not meet even if extended.
Skew lines. Two lines in space that are neither parallel nor intersecting.
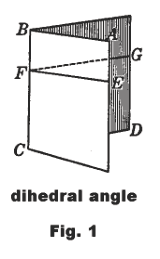
Dihedral angle. The angle formed by two intersecting planes. The two planes are called the faces, and their line of meeting the edge. See Fig. 1.
Notation for specifying dihedral angles. A dihedral angle can be named by giving a point in one face, the edge, and a point in the other face. Example. Dihedral ∠A-BC-D in Fig. 1. When there is no doubt as to the meaning, a dihedral angle can be named by specifying only its edge. Example. Dihedral ∠BC.
Plane angle of a dihedral angle. The plane angle of a dihedral angle is that angle formed by two lines, one in each face, drawn perpendicular to the edge of the dihedral angle at a point on the edge. Example. ∠EFG is the plane angle of the dihedral angle ∠A-BC-D in the figure.
Acute, right and obtuse dihedral angles. A dihedral angle is acute, right or obtuse if its plane angle is acute, right or obtuse.
Adjacent, vertical, complementary, and supplementary dihedral angles. Pairs of dihedral angles are adjacent, vertical, complementary, or supplementary if their plane angles are adjacent, vertical, complementary, or supplementary; and conversely.
Perpendicular planes. Two planes are perpendicular if the plane angle of their dihedral angle is a right angle.
Projection of a point on a plane. The foot of the perpendicular drawn from the point to the plane.
Projection of a line on a plane. The locus of the projections of all the points of the line on the plane.
Angle that an oblique line makes with a plane. The angle which an oblique line makes with a plane is the acute angle which it makes with its projection on the plane.
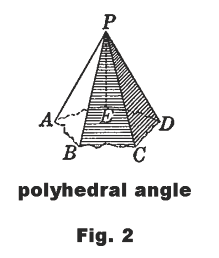
Polyhedral angle. A figure formed by three or more planes that meet in a point and are so situated that they may be intersected by another plane forming a polygon. See Fig. 2. The portions of the planes which form the polyhedral angle are called its faces, and the common point of meeting of the planes is called the vertex. The dihedral angles formed by the faces are called the dihedral angles of the polyhedral angle. The edges of the faces are the edges of the polyhedral angle.
Face angles of a polyhedral angle. The angle formed by the two edges of any particular face of a polyhedral angle is called the face angle of that face.
In Fig. 2, P is the vertex and AP, BP, CP and DP are edges of the polyhedral angle. ∠BPC is the face angle of face BPC, ∠CPD is the face angle of face CPD, and ∠B-CP-D is the dihedral angle formed by these two faces.
Notation for specifying polyhedral angles. A polyhedral angle can be specified by giving the vertex or by naming the vertex and a point on each edge. Example. Polyhedral ∠P or polyhedral ∠P-ABCDE
Names of polyhedral angles. A polyhedral angle having three faces is called a trihedral angle. Polyhedral angles of four, five, six, and eight faces are called tetrahedral, pentahedral, hexahedral, and octahedral angles respectively.
Convex polyhedral angles. A polyhedral angle is convex if the section formed by a plane intersecting all of the faces is a convex polygon.
Equal or congruent polyhedral angles. Two polyhedral angles are equal or congruent if they can be made to coincide.
Two polyhedral angles are congruent if the face angles and dihedral angles of one are equal to the face angles and dihedral angles of the other and are arranged in the same order.
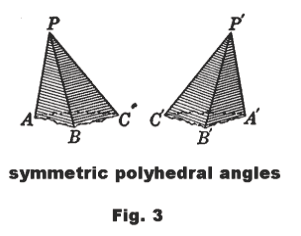
Symmetric polyhedral angles. Two polyhedral angles are symmetric if the face
angles and dihedral angles of one are equal to the face angles and dihedral angles of the other and are arranged opposite order. The two polyhedral angles of Fig. 3 are symmetric.
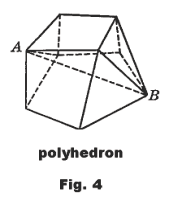
Polyhedron. A solid in three dimensions with flat polygonal faces, straight edges and sharp corners or vertices. See Fig. 4.
Diagonal of a polyhedron. A straight line joining any two vertices not in the same face.
Section of a solid. The plane figure that is formed by the intersection of a plane and a solid.
A section of a polyhedron is a polygon.
Closed prismatic surface. The surface generated by a moving straight line l which always intersects and completely traverses a fixed polygon, always remaining parallel to a fixed straight line K. The moving straight line is called the generatrix and the polygon is called the directrix. An element of the surface consists of any one position of the generatrix. An alternative definition of a prismatic surface is that it is the set of all lines passing through a fixed polygon in the direction of a fixed line K. (Line K is assumed not to lie in the plane of the polygon).
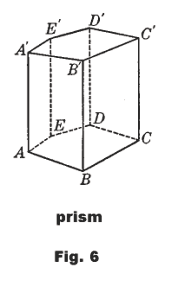
Prism. The polyhedron formed by a closed prismatic surface and two parallel planes cutting all elements. See. Fig. 6. The two sections made by the two parallel planes are the bases of the prism. Those faces of the prism that are not bases are called lateral faces. The intersections of the lateral faces are called lateral edges. The lateral area of the prism is the sum of the areas of the lateral faces. The altitude of a prism is the line segment joining the two bases and perpendicular to them i.e. the line segment representing the height of the prism.
Right section of a prism. A section made by a plane perpendicular to one of its lateral edges.
Oblique section of a prism. A section made by a plane oblique to one of its lateral edges.
Right prism. A prism whose bases are right sections i.e. a prism whose sides are perpendicular to its bases.
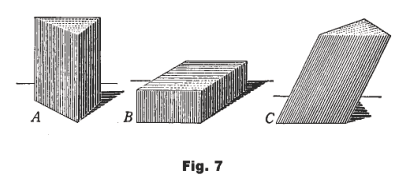
Oblique prism. A prism whose bases are not right sections i.e. a prism whose sides are not perpendicular to it bases, one whose bases are not aligned one directly above the other
In Fig. 7, prisms A and B are right prisms and prism C is an oblique prism.
Regular prism. A right prism whose bases are regular polygons.
Prisms classified by their bases. Prisms are triangular, quadrangular, pentagonal, etc., according as their bases are triangles, quadrilaterals, pentagons, etc.
Truncated prism. The polyhedron formed by a closed prismatic surface and two nonparallel planes cutting all elements.
Volume of a solid. The volume of a solid is the number of cubic units of measure enclosed by the solid. A cubic unit of measure is a cube whose edge is one linear unit long.
Congruent solids. Two solids are congruent if they can be made to coincide.
Equal (equivalent) solids. Two solids are equal, or equivalent, if they have equal volumes.
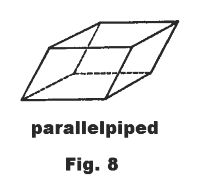
Parallelepiped. A prism whose bases are parallelograms.
Right parallelepiped. A parallelepiped that is a right prism i.e. a parallelepiped whose lateral edges are perpendicular to the bases.
Oblique parallelepiped. A parallelepiped that is an oblique prism i.e. a parallelepiped whose lateral edges are oblique to the bases.
Rectangular parallelepiped. A right parallelepiped whose bases are rectangles. Sometimes called a rectangular solid.
Cube. A rectangular parallelepiped whose edges are all equal.
Cylindrical surface. The surface generated by a moving straight line L which intersects and moves along a fixed plane curve C while remaining parallel to a fixed straight line K. The fixed curve C is called the directrix of the surface and the moving line L is called the generatrix (or generator) of the surface. An element of the surface consists of any single position of the generatrix. An alternative definition of a cylindrical surface is that it is the set of all lines passing through a fixed plane curve C in the direction of a fixed line K. (Line K is assumed not to lie in the plane of the polygon).
Cylinder. A solid formed by a closed cylindrical surface and two parallel planes cutting all elements. The parallel planes sections are the bases of the cylinder and the lateral surface is the cylindrical surface. The altitude of a cylinder is the line segment joining the two bases and perpendicular to them i.e. the line segment representing the height of the cylinder.
Right section of a cylinder. A section made by a plane perpendicular to the elements.
Right cylinder. A cylinder in which the planes of the bases are perpendicular to the elements.
Oblique cylinder. A cylinder in which the planes of the bases are oblique to the elements.
Circular cylinder. A cylinder whose bases are circles. A right circular cylinder is sometimes called a cylinder of revolution because it can be generated by revolving a rectangle about one of its sides.
Plane tangent to a cylinder. A plane is tangent to a cylinder if it contains an element and no other point of the cylinder.
Prism inscribed in a cylinder. A prism is inscribed in a cylinder when its lateral edges are elements of the cylinder and its bases lie in the planes of the bases of the cylinder. When a prism is inscribed in a cylinder, the cylinder is circumscribed about the prism.
Prism circumscribed about a cylinder. A prism is circumscribed about a cylinder when the lateral faces of the prism are tangent to the cylinder and the bases of the prism lie in the planes of the bases of the cylinder. When a prism is circumscribed about a cylinder, the cylinder is inscribed in the prism.
Similar cylinders of revolution. Cylinders generated by the revolution of similar rectangles about corresponding sides.
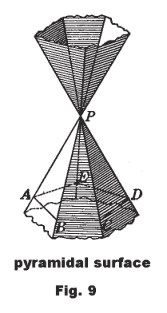
Pyramidal surface. A surface generated by a line passing through a fixed point and moving along a broken line in a plane that does not contain the fixed point. See Fig. 9. The moving line is called the generatrix and the broken line is called the directrix. It is a closed pyramidal surface if the broken line is a polygon.
A pyramidal surface consists of two parts separated by a vertex. Each of these parts is called a nappe.
Pyramid. A solid formed by one nappe of a closed pyramidal surface and a plane cutting all its elements. The base of the pyramid is the polygon shaped section of the closed pyramidal surface made by the plane. The triangular faces of the pyramid are the lateral faces. The edges where the faces meet are the lateral edges. The vertex is the vertex of the closed polygonal surface. The altitude of a pyramid is the perpendicular from the vertex to the base i.e. the line segment representing the height of the pyramid.. The lateral area of the pyramid is the sum of the areas of the lateral faces.
Pyramids classified according to their bases. A pyramid is triangular, quadrangular, pentagonal, etc. according as its base is triangular, quadrangular, pentagonal, etc. A triangular pyramid has four faces and is often called a tetrahedron.
Regular pyramid. A pyramid whose base is a regular polygon and whose altitude is perpendicular to the base at its center.
Slant height of a regular pyramid. The altitude of any of the lateral faces.

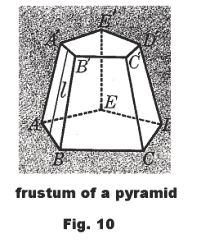
Frustum of a pyramid. The section of a pyramid between the base and a plane parallel to the base. The bases of the frustum are the base and the section made by the plane parallel to the base. The altitude of the frustum is the perpendicular between the bases. The slant height of the frustum of a regular pyramid is the altitude of any one of the lateral faces.
Conical surface. A surface generated by a line passing through a fixed point and moving along a fixed curve that does not contain the fixed point. The moving line is called the generatrix and the fixed curve is called the directrix. Alternative definition: A conical surface is a surface that is the union of all lines that pass through a fixed point and intersect a fixed curve. It is a closed conical surface if the fixed curve is closed.
Cone. A solid formed by one nappe of a closed conical surface and a plane cutting all elements — where the generatrix of the conical surface is a circular or roughly circular plane curve. The base of the cone is the section of the conical surface made by the plane, and the lateral surface is the curved part of the surface. The lateral area of a cone is the area of the lateral surface. The altitude of a cone is the perpendicular from the vertex to the plane of the base. The radius of a cone is the radius of its base.
Circular cone. A cone whose base is a circle. The axis of a circular cone is the line segment from the vertex to the center of the base.
Right circular cone. A cone whose axis is perpendicular to the plane of the base. Since a right circular cone has a surface that can be generated by the revolution of a right triangle about one of its legs as an axis, it is sometimes called a cone of revolution.
Oblique circular cone. A cone whose axis is oblique to the plane of the base.
Frustum of a cone. The section of a cone between the base and a plane parallel to the base. The bases of the frustum are the base and the section made by the plane parallel to the base. The altitude of the frustum is the perpendicular between the planes of the bases.
Slant height of a right circular cone. The length of one of its elements.
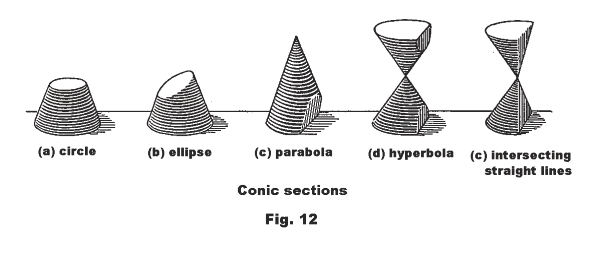
Conic section. The section of the conical surface of a right circular cone made by a plane.
The type of curve that one obtains when cutting a right circular cone by a plane depends on the position and angle of the cutting plane. The different possibilities are shown in Fig. 12.. The possibilities include (a) circle, (b) ellipse, (c) parabola, (d) hyperbola, and (e) two intersecting straight lines.
Cones. Inscribed and circumscribed pyramids. A pyramid whose lateral edges are elements of a cone and whose base is inscribed in the base of a cone is said to be inscribed in the cone. A pyramid whose lateral faces are tangent to a cone and whose base is circumscribed about the base of the cone is said to be circumscribed about the cone.
Similar cones of revolution. Cones generated by the revolution of similar right triangles about two corresponding legs as axes.
Sphere. The set of points in space at a given distance from a fixed point. The fixed point is the center; a straight line segment joining the center to any point on the sphere is the radius.
Chord of a sphere. A line segment joining any two points of the sphere.
Diameter of a sphere. A chord passing through the center of the sphere.
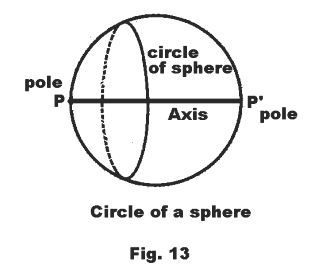
Circles of a sphere. The section of a sphere made by a plane is called a circle of the sphere. See Fig. 13. A great circle of the sphere is the intersection of the sphere and a plane through its center. A small circle of the sphere is the intersection of the sphere and a plane not passing through its center.
Axis of a circle of a sphere. That diameter of the sphere which is perpendicular to the plane of the circle. The extremities of the axis are the poles of the circle. See Fig. 13.
Pole of a circle on a sphere. A point of intersection of the sphere and the line through the center of the circle of the sphere and perpendicular to the plane of the circle. See Fig. 13.
Spherical distance between two points of a sphere. The spherical distance between two points of a sphere is the length of the minor arc of a great circle joining them.
Quadrant. One fourth of a great circle.
Polar distance of a circle of a sphere. The spherical distance from any point on the circle to its nearest pole (or to either pole if they are equally distant).
Tangent to a sphere. A line and a sphere, or a plane and a sphere, are tangent to each other if they have one and only one point in common. The common point is called the point of contact or the point of tangency.
Tangent spheres. Two spheres are tangent to each other if they are tangent to a plane at the same point.
Inscribed sphere. A sphere is inscribed in a polyhedron if it is tangent to all the faces of the polyhedron. If the sphere is inscribed in a polyhedron, the polyhedron is circumscribed about the sphere.
Circumscribed sphere. A sphere is circumscribed about a polyhedron if the vertices of the polyhedron lie on the sphere. If a sphere is circumscribed about a polyhedron, the polyhedron is inscribed in the sphere.
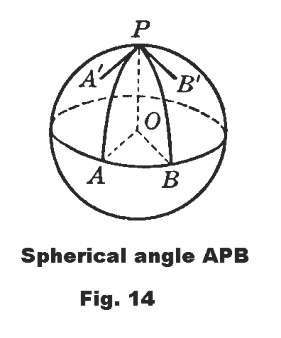
Spherical angle. The angle formed by two intersecting arcs of great circles. A spherical angle is equal to the angle to formed by the lines which are tangent to the arcs at their point of intersection.
In Fig. 14, the spherical angle is APB. It is equal to the plane angles AʹPBʹ and AOB.
Zone. A portion of a sphere included between two parallel planes. If one of the planes is tangent to the sphere and one intersects the sphere, the zone is called a zone of one base. See Fig. 15.
Bases of a zone. The circles formed by the intersections of the planes and the sphere.
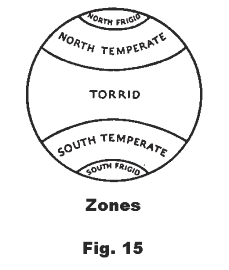
Altitude of a zone. The perpendicular distance between the planes of the zone.
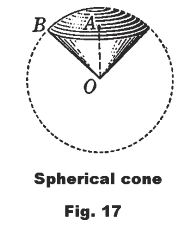
Spherical sector. A solid generated by rotating a sector of a circle about a diameter.
A sector of a circle consists of the portion of a circle bounded by two radii and the intercepted arc. Fig. 16 shows a sector of a circle and the spherical sector resulting from rotating it about a diameter.
A spherical sector has a zone as its base and the center of the sphere as its vertex.
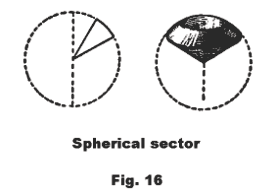
Spherical cone. A spherical cone is the conical solid formed by rotating a sector of a circle about one of the two radii. In Fig. 17 the spherical cone was formed by rotating a circle about radius OA.
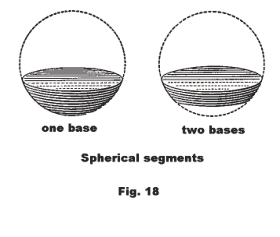
Spherical segment. The solid bounded by a sphere and two parallel planes intersecting, or tangent to, the sphere. Also, a solid bounded by a zone and the planes (or plane) of its bases. If one plane is tangent to the sphere, the spherical segment is a spherical segment of one base; otherwise, it is a spherical segment of two bases.
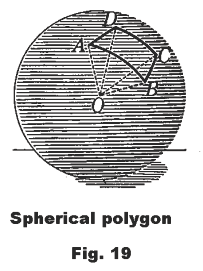
Spherical polygon. A portion of a sphere bounded by three or more arcs of great circles.
Spherical triangle. A spherical polygon of three sides. The words isosceles, equilateral, equiangular, median, etc. have the same meaning when applied to spherical triangles as when applied to plane triangles.
Poles of an arc of a circle. The poles of the circle containing the arc.
Polar triangles. The polar triangle of a spherical triangle ABC is another spherical triangle that has a certain special relationship with triangle ABC. Let AʹBʹCʹ be the polar triangle of the spherical triangle ABC. Then Δ AʹBʹCʹ is a spherical triangle which has the following property:
Property: The vertices of ΔAʹBʹCʹ are poles of the sides of ΔABC as follows: vertex Aʹ is a pole of side BC, vertex Bʹ is a pole of side AC, vertex Cʹ is a pole of side AB.
We note now that any arc has two poles: arc BC has poles P1 and P2 , arc AC has poles Q1 and Q2, arc AB has poles R1 and R2. Thus Aʹ could be either P1 or P2, Bʹ could be either Q1 or Q2, Bʹ could be either R1 or R2. Thus we see that there exists more than one spherical triangle that has the above stated property. There are, in fact, eight. The spherical triangle that is the polar triangle AʹBʹCʹ of triangle ABC is a particular one of these eight as given in the following definition:
Def. Polar triangle. The polar triangle of the spherical
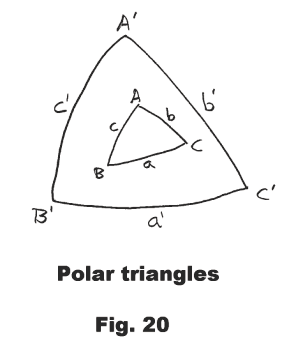
triangle ABC is the triangle AʹBʹCʹ in which Aʹ is that pole of BC whose distance from A is less than a quadrant, Bʹ is that pole of AC whose distance from B is less than a quadrant, and Cʹ is that pole of AB whose distance from C is less than a quadrant.
Complementary and supplementary spherical angles. Spherical angles are complementary when their sum is a right angle and are supplementary when their sum is a straight angle.
Complementary and supplementary arcs. Arcs of great circles are complementary when their sum is a right angle and are supplementary when their sum is a straight angle.
Kinds of spherical triangles. A plane triangle has, at most, one right angle or one obtuse angle. A spherical triangle may contain two or three right angles or two or three obtuse angles. A birectangular spherical triangle has two right angles and a trirectangular spherical triangle has three right angles.
Spherical excess of a spherical triangle. The spherical excess of a spherical triangle is the difference between the sum of its angles and the sum of the angles of a plane triangle.
Example. The spherical excess of a spherical triangle having angles of 60o, 75o, and 85o is (60o + 75o + 85o) - 180o = 40o
Spherical excess of a spherical polygon. The spherical excess of a spherical polygon is the difference between the sum of its angles and the sum of the angles of a plane polygon having the same number of sides.
The sum of the interior angles of a polygon of n sides is equal to 180(n - 2).
Example. The spherical excess of a spherical polygon having angles of 70o, 90o, 130o, and 140o is (70o + 90o + 130o + 140o) - 360o = 70o
Congruent spherical triangles. Two spherical triangles are congruent if they can be made to coincide by a rigid motion in space.
Two spherical triangles will coincide if the sides and angles of one are equal to the sides and angles of the other and are arranged in the same order.
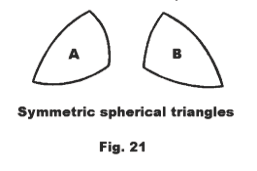
Symmetric spherical triangles. Two spherical triangles are symmetric if the sides and angles of one are equal to the sides and angles of another, but are arranged in reverse order.
In general, two symmetric spherical triangles are not congruent, because of the curvature of the sides. The triangles A and B of Fig. 21 are symmetric, but are not congruent, because they cannot be made to coincide.

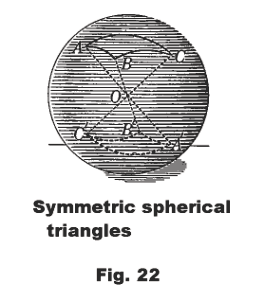
Two symmetric spherical triangles. Consider two spherical triangles ABC and AʹBʹCʹ so located on the same sphere that AAʹ, BBʹ, CCʹ are diameters. See Fig. 22. It can be proved that arc AB = arc AʹBʹ, arc BC = arc BʹCʹ, arc AC = arc AʹCʹ, ∠A = ∠Aʹ, ∠B = ∠Bʹ, and ∠C = ∠ACʹ. Examination of the triangles will show that they are symmetric.
Equal spherical polygons. Two spherical polygons are equal (or equivalent) if they have equal areas.
Spherical degree. A portion of a sphere enclosed by a spherical triangle in which two angles are right angles and the third angle is one degree.
A hemisphere contains 360 spherical degrees. A sphere contains 720 spherical degrees. The spherical degree is used in measuring and comparing the areas of spherical surfaces on the same sphere.
Semicircle. Half of a circle.
Lune. A lune is the portion of the surface of a sphere included between two semicircles.
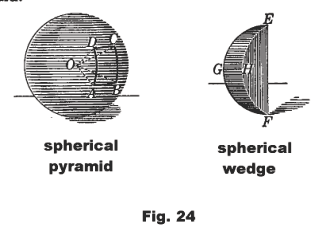
Spherical pyramid. As solid whose base is a spherical polygon and whose vertex is the center of the sphere.
Spherical wedge. A solid formed by a lune and the planes of its great circles
Polyhedrons classified by the number of faces. A polyhedron of four faces is a tetrahedron; one of six faces is a hexahedron; one of eight faces is a octahedron; one of twelve faces is a dodecahedron; one of twenty faces is an icosahedron.
Regular polyhedron. A polyhedron whose faces are congruent regular polygons and whose polyhedral angles are congruent.
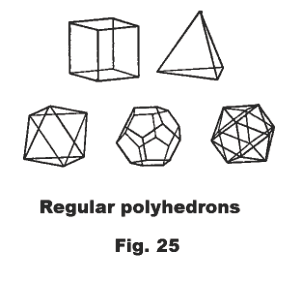
There are five regular polyhedrons. They are the tetrahedron, hexahedron, octahedron, dodecahedron, and the icosahedron. Their existence has been known since the times of the ancient Greeks and are often called the Platonic Solids.
Similar polyhedrons. Two polyhedrons are similar if they have the same number of faces similar each to each and similarly placed, and have their corresponding polyhedral angles equal.
Prismatoid. A polyhedron all of whose vertices lie in two parallel planes.
The faces that lie in the parallel planes are called the bases. Prisms, pyramids, and frustums of pyramids are special cases of the prismatoid. The altitude of a prismatoid is the distance between the parallel planes. The midsection of a prismatoid is the section made by a plane parallel to the bases and midway between them.
Postulates
1.0 Two dihedral angles are equal (or congruent) if they can be made to coincide.
2.0 The volume of a rectangular solid is the product of its three dimensions. (V = abc where a, b, and c are the dimensions.)
3.0 If a cylinder whose bases are regular polygons is inscribed in, or circumscribed about, a circular cylinder, and if the number of lateral faces of the prism is indefinitely increased,
1) The lateral area of the prism approaches the lateral area of the cylinder as a limit.
2) The volume of the prism approaches the volume of the cylinder as a limit
3) The perimeter of a right section of the prism approaches the perimeter of a right section of the cylinder as a limit.
4.0 If a pyramid whose base is a regular polygon in inscribed in or circumscribed about a circular cone, and if the number of lateral sides of the pyramid is indefinitely increased,
1) The lateral area of the pyramid approaches the lateral area of the cone as a limit
2) The volume of the pyramid approaches the volume of the cone as a limit
References
A. M. Welchons, W. R. Krickenberger. New Solid Geometry
Jesus Christ and His Teachings
Way of enlightenment, wisdom, and understanding
America, a corrupt, depraved, shameless country
On integrity and the lack of it
The test of a person's Christianity is what he is
Ninety five percent of the problems that most people have come from personal foolishness
Liberalism, socialism and the modern welfare state
The desire to harm, a motivation for conduct
On Self-sufficient Country Living, Homesteading
Topically Arranged Proverbs, Precepts, Quotations. Common Sayings. Poor Richard's Almanac.
Theory on the Formation of Character
People are like radio tuners --- they pick out and listen to one wavelength and ignore the rest
Cause of Character Traits --- According to Aristotle
We are what we eat --- living under the discipline of a diet
Avoiding problems and trouble in life
Role of habit in formation of character
Personal attributes of the true Christian
What determines a person's character?
Love of God and love of virtue are closely united
Intellectual disparities among people and the power in good habits
Tools of Satan. Tactics and Tricks used by the Devil.
The Natural Way -- The Unnatural Way
Wisdom, Reason and Virtue are closely related
Knowledge is one thing, wisdom is another
My views on Christianity in America
The most important thing in life is understanding
We are all examples --- for good or for bad
Television --- spiritual poison
The Prime Mover that decides "What We Are"
Where do our outlooks, attitudes and values come from?
Sin is serious business. The punishment for it is real. Hell is real.
Self-imposed discipline and regimentation
Achieving happiness in life --- a matter of the right strategies
Self-control, self-restraint, self-discipline basic to so much in life